Keywords: fractional, integrals, convolution, variable, quadratures, adaptive.

Integro-differential equations of fractional order have recently showed highly interesting in connections with many fields of science [3,7,8]. Infact, we consider linear equations whose prototype is

where and , which can be written in a equivalent way as

Properties concerning to the continuous solution of (59) can be found in the literature, (for example [8] and references cited there), also in a more general framework [9].

In this paper we focus on the numerical solution of (59). In this way, one can easily understand that the key to these numerical methods consists in obtaining good enough quadratures to approximate the fractional integrals as the one in (59) or (60).

Discrete solutions of (59) have been widely studied in the literature (see [1,2,6]) but unfortunately the high computational cost of the algorithm involving convolution equations, and more precisely quadratures of convolution type, sometimes makes its implementation in applications useless. Thus, the effort from the numerical point of view, must concentrate in obtaining fast and efficient quadratures in order to obtain numerical schemes which implementation could be affordable in practical applications.

The goal of our paper is the obtaining of a numerical scheme based on a variable step size quadrature which represents an extension of the quadratures considered in [1,2,6]. The obtaining of these numerical methods is based in writing (60) in a suitable way which allows us to use classical schemes for initial value problems.

The quadrature considered here is based on the variable step size backward Euler method and read as

We must notice that, this extension does not show obvious at all, in fact, variable step size quadratures loss the convolutional structure on the contrary what happens when constant step size is considered. Therefore, different ideas must be used in proofs, being the ones in the works cited above not longer valid here.

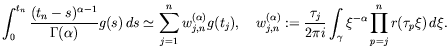
The main result of our paper provides a priori error estimates for the proposed numerical scheme. At the same time, these estimates show that, if constant step size is considered, then the numerical method exhibits, as expected in view of [1], a first order of convergence.

In the paper we show numerical experiments illustrating the theoretical results.

Open problems keep still open as, for instance, the choice of suitable or even optimal, time step settings.

1

E. Cuesta, Ch. Lubich, and C. Palencia, Convolution quadrature time discretization of fractional diffusion-wave equations, Math. Comp., 75, 673-696, 2006. doi:10.1090/S0025-5718-06-01788-1

2

E. Cuesta and C. Palencia, A numerical method for an integro-differential equation with memory in banach spaces: Convergence and qualitative properties, SIAM J. Numer. Anal., 41, 1232-1241, 2003. doi:10.1137/S0036142902402481

3

A. A. Kilbas, H. M. Srivatava, and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, 2006.

4

Ch. Lubich, Discretized fractional calculus, SIAM J. Math. Anal., 17, 704-719, 1986. doi:10.1137/0517050

5

Ch. Lubich, Convolution quadrature and discretized operational calculus. I, Numer. Math., 52, 129-145, 1988. doi:10.1007/BF01398686

6

Ch. Lubich, Convolution quadrature revisited, BIT, 44, 503-514, 2004. doi:10.1023/B:BITN.0000046813.23911.2d

7

R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: a fractional dynamics approach, Physics Reports, 339, 1-77, 2000. doi:10.1016/S0370-1573(00)00070-3

8

I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999.

9

J. Prüss, Evolutionary Integral Equations and Applications, Birkhäuser, Basel, 1993.

10

A. Schädle, María López-Fernández, and C. Lubich, Fast and oblivious convolution quadrature, (to appear in SIAM J. Sci. Comp.) doi:10.1137/050623139

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)