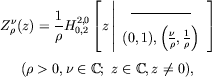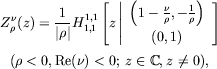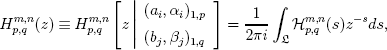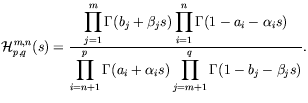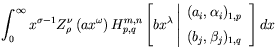engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
The Krätzel Function as the H-Function and the Evaluation of Integrals
1Department of Mathematics and Mechanics, Belarusian State University, Belarus
2Department of Applied Mathematics, Fukuoka University, Japan
3Department of Mathematics and Statistics, Jai Narain Vyas University, India
4Departamento de Análisis Matemático, Universidad de la Laguna, Spain
defined for 
,
and
, being such that
when
,
by
This function, coinciding for
and 
with the
McDonald function
apart from the power function:
for
was introduced by Krätzel. Properties of the
function (26) with 
were investigated by some
authors. In particular, the explicit solutions of some ordinary and
partial differential equations of fractional order were obtained in
terms of
. Such investigations now are of a great
interest in connection with applications,
We establish the formula for the Mellin transform of
:
provided that
,
and
are such that
when , while
when 
.
Using (28) we extend
from positive
to complex z by means of its representation in terms of the
H-function in the form
when
while for 
and give conditions for these representations.
Note that for integers
such that
and for
and
the function
is defined via a
Mellin-Barnes integral in the form
An empty product in (32), if it occurs, is taken to be one.
in (31) is an infinite contour which separates
all poles of the Gamma functions
to the left and all poles of the Gamma functions
to the right of
.
Using (29) and (30), we find the
asymptotic estimates for
at zero and infinity.
Our results in the case give more precisely the known
asymptotic relations for
as 
and as
We apply the obtained results to evaluate the integral
with
,
and
involving the function
and the
H-function in the integrand. We prove that the integral
(31) is the H-function of the form
and
for
and respectively. The special cases of such
formulas are presented when
coincides with the
Meijer G-function. Applications are given to evaluate integrals
involving a product of
and the Bessel function
of the first kind
, the McDonald function
,
the Whittaker confluent hypergeometric function
and the Gauss hypergeometric function
. Special cases involving products of
and elementary functions are also presented.
It should be noted that there are many known integrals of special functions that can be evaluated in terms of elementary and special functions. The integrals evaluated in this paper are new.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)