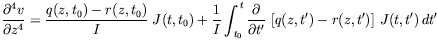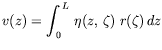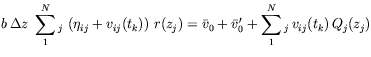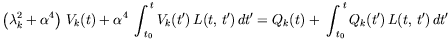Keywords: viscoelasticity, Bernoulli Navier beam, elastic media, contact problem, numerical solution, Boussinesq model, Winkler model, analytical solution.

A Bernoulli Navier beam with viscoelastic behavior is considered. The beam is subject to static loads and rests on an elastic medium. As regards the last, attention is focused on Boussinesq's and Winkler's models. Many engineering materials exhibit a constitutive law depending on time, that is they have a viscous behavior. This can influence the static behaviour of a beam resting on an elastic medium. This is a problem that to the authors' knowledge has had little attention.

As regards the beam, even if it is in a plane stress state and the shear deformability is disregarded, from a theoretical point of view, if the beam is homogeneous, the viscoelastic constitutive law requires the knowledge of two functions, that is the volumetric and the deviatoric creep functions. These functions can be replaced by the uniaxial creep function and the viscous Poisson ratio . However, for many materials such as concrete the last can be considered independent of time as will be assumed here.

By applying the usual assumptions of linear viscoelasticity and plane section law, the beam equilibrium is governed by the following integrodifferential equation:

where is the second moment of the area of the beam transverse section, the external load, and the distributed load exchanged by the beam and the elastic medium. By integrating (50) per parts, the alternative form is found:

where is the viscous kernel, and E is the elastic modulus of the beam.

The compatibility between the displacements of the beam axis and the superior surface of the Boussinesq's elastic medium requires that the following integral equation is satisfied:

where is beam length, and the Green function, for which here it assumed . An analytical solution of Equations, (51,52) is hardly conceivable. In the present paper, the problem is discretized in both time and space, and a solution procedure is proposed, which avoids the direct numerical integration of (51). For each time instant a set of algebraic equations is solved of the form

in which , are fictitious restraint displacement and rotation, , are influence coefficients for the soil and the beam, respectively, the last being computed taking creep into account.

A Winkler's medium does not transmit shear, and the interface load is given by

After substituting Equation (54) in (51), separating the variables, a solution is looked for in the form of an infinite series as

The functions must satisfy the boundary conditions, and constitute a complete ortho-normal basis in . It is emphasized that the eigenfunctions of the free vibrations of the same beam have such features. After some algebra, the infinite set of Volterra's integral equations is

where are the eigenvalues of the free vibration problem, , and . Equation (56) admits an analytical solution. This is given in close form when the creep law is either hereditary or of pure aging type. In this second case, the creep kernel is that suggested by Dischinger, Krall, and Whitney, which depends on the loading time only, that is . The numerical example compares the responses of a beam resting on a Winkler soil for both hereditary and aging behavior.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)