
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Calculation of Eigenvalues of a Piezoelastic Beam with the Pseudospectral Method
Centre for Advanced Materials, Manufacturing and Prototyping Research, Department of Mechanical Engineering, Durban Institute of Technology, South Africa
Analytical and approximate methods have been implemented with great success in solving the differential equation of motion of piezoelastic structures. These include the classical method [1], Fourier analysis [2], Green's method [3], finite element method [4], amongst others. However, the literature reviewed in the field of piezoelastic structures is devoid of the use of the pseudospectral method in solving the piezoelastic differential equations. Very few articles in solid mechanics use this method compared with those in fluid mechanics [5]. This study contributes by solving the same using the psuedospectral method. The method is elegant, highly accurate and does not require mathematical rigour of the methods mentioned above.
The study considers the free vibration problem of a piezoelastic beam. The differential equation of motion is derived based on the Euler beam theory. The kinematic behaviour is represented by the variable ![]() , which represents the deflection of the neutral axis of the beam. The variable separable technique is used, i.e.
, which represents the deflection of the neutral axis of the beam. The variable separable technique is used, i.e.
![]() , and a sinusoidal motion in time
, and a sinusoidal motion in time ![]() is assumed for the temporal function
is assumed for the temporal function ![]() . The spatial differential eigenvalue problem is then solved using the pseudospectral method. Following a simple procedure described below, the method is guaranteed to give an error which decreases exponentially fast with
. The spatial differential eigenvalue problem is then solved using the pseudospectral method. Following a simple procedure described below, the method is guaranteed to give an error which decreases exponentially fast with ![]() , the number of degrees of freedom. The method first chooses a set of spectral basis functions
, the number of degrees of freedom. The method first chooses a set of spectral basis functions
![]() that satisfy the boundary conditions. Next, it approximates the eigenfunction
that satisfy the boundary conditions. Next, it approximates the eigenfunction ![]() by the
by the ![]() -term truncation of the spectral series with unknown coefficients
-term truncation of the spectral series with unknown coefficients ![]() . That is
. That is
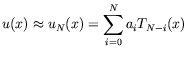 |
(49) |
where the basis functions
If the eigenmodes are needed, they may be evaluated by substituting the appropriate matrix eigenmode as the coefficients of ![]() and then summing the series at each point of the graph. The
and then summing the series at each point of the graph. The ![]() -dimensional descretisation matrix of the differential equation usually has
-dimensional descretisation matrix of the differential equation usually has ![]() eigenvalues. Not all the matrix eigenvalues will be good approximations to those of the differential equation. Numerical results show that one typically obtains about
eigenvalues. Not all the matrix eigenvalues will be good approximations to those of the differential equation. Numerical results show that one typically obtains about ![]() matrix eigenvalues that are a close approximation of those of the differential equation.
matrix eigenvalues that are a close approximation of those of the differential equation.
With a bit of care, the pseudospectral method is a very robust and efficient method for solving linear differential eigenvalue problems. The exponential rate of convergence with ![]() implies that it is possible to distinguish acceptable eigenvalues from unacceptable eigenvalues. Also, it is easy to program and check than the hand-derivation of the analytic type solution.
implies that it is possible to distinguish acceptable eigenvalues from unacceptable eigenvalues. Also, it is easy to program and check than the hand-derivation of the analytic type solution.
- 1
- M. Kekana, P. Tabakov and M. Walker, "A shape control model for piezo-elastic structures based on divergence free electric displacement", International Journal of Solids and Structures, 40, 715-727, 12003. doi:10.1016/S0020-7683(02)00611-X
- 2
- H.S. Tzou, Y. Bao and V.B. Venkayya, "Parametric study of segmented transducers laminated on cylindrical shells, part 1: Sensor patches", Journal of Sound and Vibration, 97(2), 207-224 1996. doi:10.1006/jsvi.1996.0526
- 3
- S. Adali, I.S. Sadek, J.C. Bruch, Jr, J.M. Sloss, "Orthotropic piezoelectric patches for control of symmetric laminates via an integral equation", Composite Structures, 62, 271-277, 2003. doi:10.1016/j.compstruct.2003.09.025
- 4
- M. Kekana, "Finite element modelling of laminated piezo-elastic structures: Lyapunov stability analysis", Journal of Sound and Vibration, 256(3), 463-473, 2002. doi:10.1006/jsvi.2002.5000
- 5
- J.P. Boyd, "Chebyshev and Fourier spectral methods", 2
 edition, Dover Publications, 2000.
edition, Dover Publications, 2000.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)