
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Stress Analysis and Failure Theory in Piezoelectric Materials
Department of Engineering Mechanics, Shanghai Jiaotong University, Shanghai, P.R. China
From the thermodynamics a simple method is used to derive the
fundamental equations [1,2]. For static and small deformation problems the
electric Gibbs free energy ![]() in general can be written as
in general can be written as
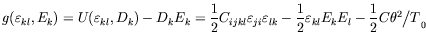 |
|
(higher order terms) |
(47) |
From the thermodynamic theory, the constitutive equations can be obtained. The equilibrium equation can be obtained from a variational principle and the following fundamental equations can be obtained:
in considered body |
in environment |
on interface |
All applied fundamental equations in piezoelectric and electrostrictive materials are enclosed in above equations These governing equations are first clearly given. The above theory is especially important for the stress analysis of electrostrictive materials, because in previous literature it is very confusing.
The general properties of anisotropic eigentensors for any anisotropic piezo-elasticity possesses the following properties [3]: For any piezo-elastic symmetry, the generalized stress and strain tensor can be additively decomposed into a sum of nine or fewer eigentensors (spectral decomposition); For any piezo-elastic symmetry, each eigenstress is directly proportional to associated eigenstrain and independent on other eigenstrain (decoupling property); Any modal energy is a scalar-valued product of the eigenstress and associated eigenstrain. The different modal energies do not interact with each other. A new failure criterion based on modal strain energy can given as follows:
When a linear combination of all modal strain energy ![]() at an arbitrary point
in the material reaches a critical value
at an arbitrary point
in the material reaches a critical value ![]() .
.
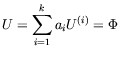 |
(48) |
the failure has occurred at that point. Where
In the theory of surface acoustic wave propagation in the biasing state, we obtain the general fundamental dynamic equations in a finite deformation [4], which are the more correct equations in the current literature. The effects of biasing, initial stress on the wave propagation velocity and other properties of Love wave, Lamb wave, Rayleigh wave and B-G wave are discussed.
Using the extended Eshelby-Stroh formulation and analytical continuation method the problem of the interface crack in bi-piezothermoelastic material with point heat source was reduced to a Hilbert problem [5]. The whole field solutions of temperature, heat flux, displacement, electric field, stress, electric induction and stress electric intensity factors are all obtained. The interaction between the interface cracks and a point source is also given. In [6], Green's functions for an infinite piezoelectric media with an elliptic piezoelectric inhomogeneity are given for a generalized electro-mechanical force and a generalized electro-mechanical line dislocation that may be located outside, inside or on the interface of elliptic boundary of inhomogeneity. The interaction forces on the dislocation owing to the existence of the inhomogeneity are also given.
- 1
- L.D. Landau, E.M. Lifshitz, Electrodynamics of Continuum Media, Pergamon Press, Oxford,1960
- 2
- Z.B. Kuang, Nonlinear continuum mechanics. Shanghai Jiaotong University Press, Shanghai.(in Chinese), 2002
- 3
- Z. B. Kuang, Z. D. Zhou, Y. Chen and S. X. Zhao, Eigen-material constants, mode and failure criterion for piezoelectric media. Int.J.Appl.Electrom.18: 235-250, 2003.
- 4
- J. Su., Z. B. Kuang, H. liu, Love wave in ZnO/SiO
 /Si structure with initial stresses. Journal of Sound and Vibration, 286: 981-999, 2005. doi:10.1016/j.jsv.2004.10.040
/Si structure with initial stresses. Journal of Sound and Vibration, 286: 981-999, 2005. doi:10.1016/j.jsv.2004.10.040
- 5
- S. P. Shen, Z.B. Kuang, Interface crack in bi-piezothermoelastic media and the interaction with a point heat source. Int J Solids Struct 35 (30): 3899-3915, 1998. doi:10.1016/S0020-7683(97)00208-4
- 6
- Z.Y. Huang, Z. B. Kuang, Dislocation inside a piezoelectric media with an elliptic inhomogeneity. Int J Solids Struct 38 (46-47): 8459-8479, 2001. doi:10.1016/S0020-7683(01)00062-2
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)