Keywords: stochastic, finite fault, omega-square, simulation, spectra decay parameter, quality factor, elastic response spectra.

To adequately design an earthquake resistant structure, designers need to know the dynamic characteristic of the estimated ground motion particularly in non-linear analysis for a given location. In principal, ground motions are predicted by identifying the major regional faults (or source zones) and propagating the generated seismic waves from the ruptured sources to the site of interest.

Acceleration time histories, recorded during the destructive 22 February 2005 (M6.4) Zarand earthquake, have been simulated using a stochastic modelling technique using the finite fault method proposed by Beresnev and Atkinson [1,2]. In this method, the finite fault plane is subdivided into elements, each element is assigned a stochastic spectrum based on the method proposed by Boore [3], and the delayed contributions from all subfaults are summed in the time domain. The recorded earthquake at Zarand station, which was 17 km from the epicentre was simulated as the first step. In the second step the results were validated with those of the observed event. The comparison was carried out with the strong motion acceleration time history, acceleration, velocity and the displacement elastic response spectra.

Finite-fault effects contribute not only to the duration and directivity of the ground motion; but also affect the shape of the spectra of the seismic waves. In this method, the classic Fourier spectrum of the ground acceleration near a point dislocation (an spectrum) is given by the function , where is the angular frequency and is the corner frequency [1]. At low frequencies (below ), the spectrum rises with frequency, whereas at high frequencies (above ) and until a frequency of 5 to 10 Hz, the spectrum is constant. The fault plane is discreet and divided into a certain number of equal rectangular elements (sub faults) with dimension . The sub-fault sizes increase linearly with an increase in the seismic moment magnitude of the simulated earthquake [2]. Each sub-fault is then treated as a point source with an -square spectrum, which can be fully defined by two parameters: the seismic moment and the corner frequency of the sub-fault spectrum.

In this methodology, modelling of the finite source requires information on the orientation and the dimensions of the fault plane [1,2], as well as information on the dimensions of the subfaults and the location of the hypocenter. The material properties are described by the density, , and shear wave velocity, , which were given the values 2.8 gr/cm³ and 3.5 km/sec, respectively. Another input parameter is the stress drop parameter that it is known to have large uncertainties for past events and even larger for future ones, and we decided to keep its value fixed at 50 bars [1].

The propagation model includes parameters for the geometric spreading, the anelastic attenuation, and the near surface attenuation, as well as site amplification factors. For the geometric attenuation, an operator was applied, and the anelastic attenuation was represented by a mean path-frequency-dependent quality factor, . Such factors for different Zarand stations are evaluated to be used in the simulation technique. The simulated peak ground acceleration time histories and the elastic response spectra are depicted in the paper. The effect of the near surface attenuation was also taken into account by diminishing the simulated spectra by the factor . The alluvium of the Zarand station was estimated to be soft soil with a shear wave velocity of around 300 m/s. The site amplification factor was calculated based on this shear wave velocity using the relationship proposed by Boore and Joyner [4].

We simulated the strong motion acceleration time history recorded during the 2005 Zarand destructive earthquake, using the stochastic finite-fault method [1,2]. The results were validated with those of the observed data. A good agreement was shown between the simulated and observed earthquakes which confirm that, the selected and calculated source parameters were satisfactorily reliable. In this paper, the peak ground accelerations obtained and the acceleration response spectra were shown to be insensitive with respect to the coefficients of the frequency dependent anelastic attenuation, , due to the distance of stations from the source.

The validity of the model confirms that, it can be used for generating strong motion time histories to be used in the linear and nonlinear analysis of structures such as the essential oil industrial buildings in Iran.

1

I.A. Beresnev, G.M. Atkinson, "Modeling finite-fault radiation from the 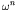spectrum", Bull. Seism. Soc. Am. 87, 67-84, 1997.

2

I.A. Beresnev, G.M. Atkinson, "FINSIM - a FORTRAN Program for Simulating Stochastic Acceleration Time Histories from Finite Faults", Seism. Res. Let. 69, 27 - 32, 1998a.

3

D.M. Boore, "Stochastic simulation of high-frequency ground motion based on seismological model of the radiated spectra", Bull. Seism. Soc. Am. 73, 1865-1894, 1983.

4

D.M. Boore, Joyner, "Site Amplification for Generic Rock Sites", Bull. Seism. Soc. Am. 87, 327 - 341, 1997.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)