
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Analysis of the Wind Dynamic Response of Towers and Metallic Masts
1Department of Civil Engineering, Instituto Politécnico de Viseu, Portugal
2Department of Civil Engineering, Faculty of Engineering (FEUP), University of Porto, Portugal
The average structural response is predominantly in the direction of the wind, but the
fluctuation response occurs either in the direction of the wind or normal to the wind. The peek
response, ![]() , can be obtained by the following expression:
, can be obtained by the following expression:
| (40) |
in which
The force of the wind can be decomposed into the sum of a constant part and a fluctuation part (Barros [2] and Holmes [4]):
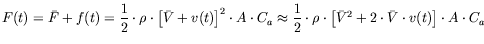 |
(41) |
For a telecommunications tower for which
![]() and
and
![]() are
respectively the tower width variation and the wind speed variation along the
normalized height
are
respectively the tower width variation and the wind speed variation along the
normalized height ![]() , the average wind force in the structure at a normalized height
, the average wind force in the structure at a normalized height
![]() can be obtained from the following expression
can be obtained from the following expression
| (42) |
in which
Any average response can be determined using the expression
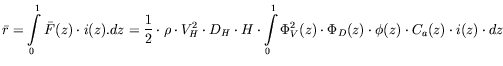 |
(43) |
where
The fluctuation part (or standard deviation part) of the wind force at a
normalized height ![]() , can be expressed by:
, can be expressed by:
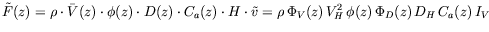 |
(44) |
in which
Some structural responses of a typical metallic tower under wind actions, determined by Almeida and Barros [1], are presented herein using the procedure described previously. Results obtained are represented graphically showing the values of each one of the responses (average, resonant and non-resonant), as well as percentage-wise the portions of response (average constant and fluctuation dynamic) associated with base shear, base moment and the tip lateral displacement.
In the design of metallic towers the wind action is usually the more limiting one. The consideration of the dynamic fluctuation effects in the design of these structures is quite essential. The effect of the resonant component in the total response is quite significant and it cannot be neglected (namely in the determination of the top displacement, where this component of the response assumes values greater than those of the non- resonant response). This conclusion is coherent with regulatory codes that suggest the resonant response should be considered in structures with fundamental frequency less than 1 Hz.
- 1
- Almeida, R.F. and Barros, R.C., "Análise do Efeito Dinâmico do Vento em Torres e Mastros Metálicos", V Congresso de Construção Metálica e Mista, Centro de Congressos de Lisboa, 24-25 de Novembro de 2005, Lisboa, Portugal (in portuguese).
- 2
- Barros, R.C., "Dimensionamento estrutural de mastros metálicos", Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 18, 3, pp. 351-365, 2002.
- 3
- Davenport, A.G., "How can we simplify and generalize wind loads?", Journal of Wind Engineering and Industrial Aerodynamics, Vol. 54/55, pp. 657-669, 1995. doi:10.1016/0167-6105(94)00079-S
- 4
- Holmes, J.D., "Along-wind response of lattice towers - II: Aerodynamic damping and deflections", Engineering Structures, Vol. 18, No. 7, pp. 483-488, 1996. doi:10.1016/0141-0296(95)00131-X
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)