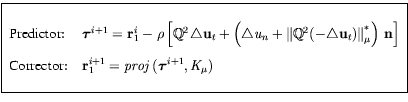engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Simulation of Orthotropic Frictional Contact with Non-Associated Sliding Rule
1Laboratoire de Mécanique de Lille, Villeneuve d'Ascq, France
2Laboratoire de Mécanique d'Évry, University d'Évry, France
3Laboratoire de Génie Civil et Génie Mécanique, Institut National des Sciences Appliquées de Rennes, France
4Institute of Fundamental Technological Research, Polish Academy of Sciences, Warsaw, Poland
The asperity model used by Micha![]() owski and Mróz [3,4] to
study anisotropic frictional contact phenomenon generates limit
friction curves in the contact plane that can be slightly
non-convex but very close to ellipses. Here, we consider only a
convex friction cone
owski and Mróz [3,4] to
study anisotropic frictional contact phenomenon generates limit
friction curves in the contact plane that can be slightly
non-convex but very close to ellipses. Here, we consider only a
convex friction cone
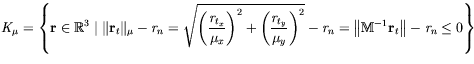 |
(36) |
where
| (37) |
is defined by the convex slip potential
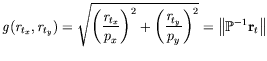 |
(38) |
where
| (39) |
where we use the dual norm
where
In this work, we propose a benchmark test to validate the algorithm for a class of non-associated anisotropic friction laws. The test of such frictional contact laws requires a 3D finite element model. The problem under consideration is a deformable elastic cylinder. The lower face is in contact with a rigid horizontal surface with anisotropic friction condition, while the upper face is subjected to a vertical rigid motion.
- 1
- G. de Saxcé, Z.Q. Feng, "New inequality and functional for contact friction : The implicit standard material approach", Mechanics of Structures and Machines, 19,301-325, 1991. doi:10.1080/08905459108905146
- 2
- M. Hjiaj, G. de Saxcé, Z. Mróz, "A variational-inequality based formulation of the frictional contact law with a non-associated sliding rule", European Journal of Mechanics A/Solids, 21, 49-59, 2002. doi:10.1016/S0997-7538(01)01183-4
- 3
- R. Michalowski, Z. Mróz, "Associated and non-associated sliding rules in contact friction problems" Archives of Mechanics, 11, 259-276, 1978.
- 4
- Z. Mróz, S. Stupkiewicz, "An anisotropic friction and wear model", International Journal of Solids and Structures, 31, 1113-1131, 1994. doi:10.1016/0020-7683(94)90167-8
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)