For the purpose of this research, a computationally efficient numerical model entitled for the Dynamic Bridge-Train Interaction (DBTI) was developed. This model is based on the finite element method and incorporates three-dimensional train and bridge subsystems. They are treated as separate subsystems coupled by the interaction forces and the compatibility of the displacements at the points of contact. The train is represented by a composition of railway vehicles with twenty-seven degrees of freedom. Each railway vehicle consists of rigid bodies, lumped masses and spring/dashpot units. The bridge is modelled with beam type finite elements, which can represent three-dimensional displacements of the structure. The resulting two sets of the equations of motion are integrated numerically by applying Newmark's method combined with an iterative procedure to incorporate the bridge-train interaction and to improve the accuracy of the solution. The model was verified by comparison with analytical and numerical solutions available in the literature and very good agreement was found.

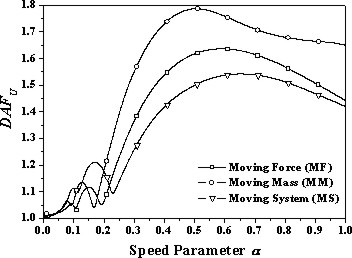
The dynamic response of railway bridges subjected to moving trains is influenced by a number of factors such as the speed of the loads, the natural frequencies of the bridge and the railway vehicles composing the train, the exciting frequency of the train, the inertia of the two systems, the damping of the bridge and the vehicles among the others. In order to study the influence of these factors a parametric analysis was carried out using non-dimensional parameters such as the speed parameter, the frequency parameter, the mass parameter, the damping ratio of the bridge and the vehicle. The dynamic response of the bridge was described by means of the dynamic amplification factor (DAF) and the mid-span acceleration of the bridge. The dynamic response of a simply supported beam for various types of the load models is shown in Figure 237.1.

Figure 237.1: The DAFU for various types of the load models versus speed parameter alpha.	Figure 237.2: The Nore Viaduct in Thomastown (photo courtesy of R. Gallagher)

The DBTI model was also applied to analyse a real-life case of a railway bridge subjected to the passage of a cargo train. The bridge under consideration was the Nore Viaduct located near Thomastown in Ireland, shown in Figure 237.2.

The parametric analysis carried out in this study shows that the DAFs generally increase with the speed parameter, however, it is not a constant trend and some local fluctuations happen. The values of DAF calculated from the displacements are higher than DAF calculated from the stresses, meaning that the values of the dynamic factors given in the design codes can be conservative in some cases. The values of DAFs are highly dependent on the type of the load model (moving force, moving mass or moving system) used in the analysis and the difference can reach 18%. Increase in the frequency parameter leads to increase of the dynamic response, by means of both, the DAF and the acceleration. The acceleration generally increases with the mass parameter. Introduction of bridge damping into the analysis can significantly decrease the acceleration, particularly for higher values of speed parameter. The DAF is not so susceptible to the damping, however it also reduces with the increase of the damping ratio. The vehicle damping has less influence on the dynamic response of the bridge than the other parameters.

The analysis of the Nore Viaduct subjected to the moving cargo train was carried out and its dynamic performance was assessed using the criteria given by Eurocode 1. It was found that for equal and close spacing of the train's axles in combination with a low fundamental frequency of the bridge caused resonance vibrations at the speed well below the maximum operational speed on the line. However, both the dynamic amplification factor and the bridge deck accelerations were within acceptable limits. It shows that the train considered can safely operate over the Nore Viaduct, without the risk of excessive dynamic effects. It is worth emphasizing that the DBTI model performs the calculations much more efficiently than general finite element packages and is equipped with a user friendly front-end, which facilitates its use by bridge engineers.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)