Keywords: analysis, arches, buckling, curved-beam element, elastic supports, nonlinear, postbuckling.

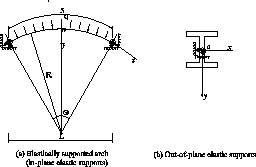
When an arch is supported on elastic foundations and, or by other structure members, the elastic foundations and, or other structural members provide elastic supports to the arch (Figure 1). The elastic supports work together with the arch to resist the external loading and so the stiffness of the elastic supports significantly influences the structural behaviour of the arch. Similar to pinned and fixed arches, an elastically supported arch that is subjected to in-plane loading may suddenly buckle in an in-plane bifurcation or snap-through mode or an out-of-plane bifurcation mode. Classical solutions for out-of-plane buckling of pinned and fixed arches that are subject to uniform bending or uniform compression were formulated by a number of researchers as summarized in Pi et al. [1], while the nonlinear in-plane buckling of pinned and fixed arches that are subjected to uniform radial loads or a central concentrated load were studied by Pi et al. [2] and Bradford et al. [3]. The linear elastic buckling of arches under general loading can be obtained using an eigenvalue analysis associated with finite element methods [1]. It is known that in the classical and eigenvalue analyses, the effects of the prebuckling deformations on buckling are ignored. However, the prebuckling deformations of shallow arches, particularly elastically supported shallow arches, are substantial, and so ignoring the effects of prebuckling deformations may lead to incorrect predictions of the buckling behaviour of elastically supported arches. Another drawback of the classical and eigenvalue analyses is that they cannot predict postbuckling responses. To describe the buckling and postbuckling behaviour of elastically supported arches correctly, finite element methods for the nonlinear large deformation analysis of elastic supported arches can be used. This paper presents a three-dimensional curved-beam element for the nonlinear large deformation analysis of elastically supported arches and to use the curved-beam element to investigate their in-plane and out-of-plane buckling and postbuckling.

A three-dimensional curved-beam element for the nonlinear large deformation analysis of elastically supported arches was formulated and used to investigate the in-plane and out-of-plane buckling and postbuckling behaviour of elastically supported arches that are subjected to a radial load uniformly distributed around the arch axis. It has been found that the stiffness of the elastic supports influences significantly the in-plane and out-of-plane buckling and postbuckling behaviour of the arch. It has also been found that the prebuckling deformations of shallow arches, particularly elastically supported shallow arches, are substantial, and that ignoring the effects of prebuckling deformations will lead to incorrect predictions of the in-plane and out-of-plane buckling and postbuckling behaviour of elastically supported shallow arches. For shallow arches, the classical buckling load has large discrepancies with the buckling load by nonlinear analysis. For non-shallow arches, the effects of prebuckling deformations on in-plane and out-of-plane buckling of an arch are quite small and so can be ignored. For non-shallow arches, the classical out-of-plane buckling load is the same as that for nonlinear analysis. After out-of-plane buckling of a non-shallow arch, the elastic load carrying capacity continues to increase until a spatial snap-through buckling occurs.

1

Pi, Y.-L., Bradford, M.A., Trahair, N.S. and Chen, Y.Y. "A further study of flexural-torsional buckling of elastic arches", International Journal of Structural Stability and Dynamics, 5(2), 163-183, 2005. doi:10.1142/S0219455405001568

2

Pi, Y.-L., Bradford, M.A., and Uy, B. "In-plane stability of arches", International Journal of Solids and Structures, 39(2), 105-125, 2002. doi:10.1016/S0020-7683(01)00209-8

3

Bradford, M.A., Uy, B., and Pi, Y.-L. "In-plane elastic buckling of arches under a central concentrated load", Journal of Engineering Mechanics, ACES, 128(7), 710-719, 2002. doi:10.1061/(ASCE)0733-9399(2002)128:7(710)

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)