Keywords: Dirichlet boundary conditions, finite element method, engineering practice, mesh generation, optimisation, software, elimination.

The paper presents an efficient way of implementing general Dirichlet boundary conditions in a finite element modeller. The proposed method of applying and processing the boundary conditions is computationally efficient and memory economical, because all constraint degrees of freedom (DOF) are eliminated already during assembly of structural global stiffness matrix and load vectors. The adopted concept has wide range of use and several possibilities are discussed at the end of the paper. It was successfully implemented in a finite element package ATENA [1]. This software is used for computing a some sample analyses to document the effectiveness of the presented method.

The actual form of the proposed Dirichlet boundary condition (BC) is:

and is -th (slave) and -th (master) DOF, e.g. displacement, , , is a constant part and coefficient in the BC. stands for total number of structural DOFs. Note that or even , (i.e. a recursive formulation) are permissible. Also, may be a free DOF and/or it can be fixed in a similar way as . Writing down Equation (31) for all constraint degrees of freedom yields a set of linear algebraic equations that is solved by Gaussian elimination. This elimination detects all redundant BCs or BCs specified in recursive manner. The problem associated matrix has sparse character and a special solver was developed to take advantage of this property. This maintains RAM and CPU requirements negligible. There exist at least three main advantages of adopting this approach:

1. Formulation and processing of a (possibly very complex) BC for 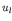is simple and is separated from definition of other BCs.
2. A particular boundary equation of the form (31) can be recursive.
3. Multiple BCs [1] can be written for the same 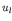. The solver will automatically detect, which of them (if any) are contradictory and which are redundant. The former ones will be applied (after warning) in a summed form, whilst the latter ones are simply ignored.

Application of the above concept of Dirichlet boundary conditions is very large. In the following some of the most important cases are mentioned.

When a structure with a complex shape is to be modelled, it must be subdivided into several substructures, each of them having a less complicated shape. Such a sub-structure, (often called macro element), is more easily meshed with an available finite element generator. However, a common problem with this concept is how to link the individual substructures together. (Note that macro elements use separate sets of finite nodes and possibly also incompatible element meshes). Application of a proper form of (31) will solve the problem.

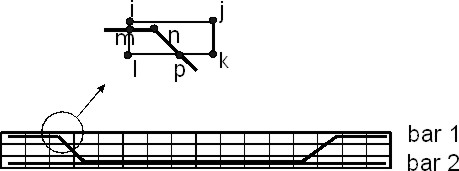
A typical reinforced concrete structure is reinforced by a large number of discrete reinforcement bars of complicated shapes. It is nearly impossible to use the same set of finite nodes for both reinforcement bars and ambient solids of concrete. It is much easier to use separate sets and link them together with help of BCs [1].

Some more examples are discussed in the full length paper, together with an analysis from engineering practice.

1

J. Cervenka and L. Jendele, "Atena User's Manual, Part 1-7", Prague: Cervenka Consulting, 2000-2006.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)