Keywords: finite element shell modelling, four-node shell element, enhanced assumed strain method.

Since the initial work of Simo and Rifai [1] many finite elements based on the enhanced assumed strain (EAS) method have been developed. As concerning shell formulations, the EAS method has been basically been used in two different manners: (i) to obtain shell and solid-shell formulations that account for through-the-thickness stretching, and (ii) to obtain shell and solid shell elements with improved membrane performance. Many linear and nonlinear EAS shell formulations (elements) have been presented, see for example Vu-Quoc and Tan [2] and the references therein.

In approach (i) the authors used the EAS method to introduce the through-the-thickness stretching parameter. Doing so, they derived attractive higher-order seven-parameter shell or solid-shell formulations, which are suitable for easy implementation of three-dimensional hyperelastic and elasto-plastic constitutive equations. On the other hand, in approach (ii) the authors used the EAS method to improve the in-plane behaviour of higher-order shell or solid-shell elements or the membrane behaviour of standard five-parameter shell elements.

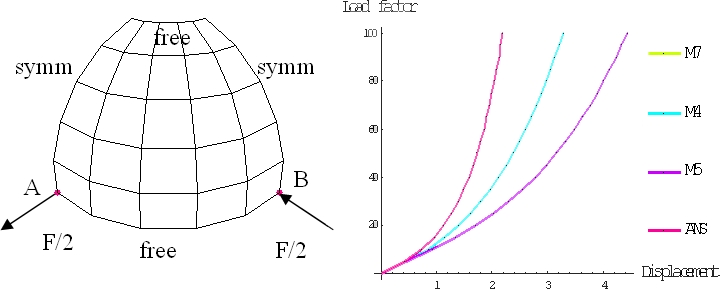
In this work we conentrate on five-parameter shell elements based on the shell theory with Reissner-Mindlin kinematics. We are interested in a robust geometrically exact four-node quadrilateral finite element for nonlinear and large rotation analysis that can give good results even for coarse and distorted meshes. We look for an element that could be effectively used in nonlinear shell shape optimization problems, see for example Kegl and Brank [3], where many iterations are required to obtain an optimized shape, and meshes may become very distorted during the optimization process. To that end, performance of the shell four-node finite element, which uses an assumed natural strain (ANS) concept to avoid the shear locking and displacement formulation for the membrane and the bending parts of the corresponding functional, is improved by the use of the EAS method. Within the EAS method both the membrane and the bending strains of the element are enhanced. In order to check for an optimal four-node EAS-ANS shell element, several possibilities for an enahncement of membrane and bending strains have been studied and coded. In contrast to the usual approach, we make an enhancement of both the membrane and the bending strains. Four, five or seven parameters are used to define enhanced membrane strains, and the same number of parameters is used to enhance the bending strains. For the transverse shear strains the ANS method is used. To obtain derivatives of the corresponding EAS functionals with respect to the independent finite element parameters, we used symbolic manipulation and an automatic differentiation tool developed by Korelc [4].

Numerical examples show that an enhancement of the bending strains does not improve the performance of a four-node shell finite element for a typical bending dominated problem. They also show that four enhancement parameters are not enough, and that five and seven enhancement parameters give equal numerical results.

1

J.C. Simo and S. Rifai, "A class of mixed assumed strain methods and the method of incompatible modes", Int. J. Numer. Meth. Engng., 29, 1595-1638, 1990. doi:10.1002/nme.1620290802

2

L. Vu-Quoc and X.G. Tan, "Optimal solid shells for non-linear analyses of multilayered composites. I. Statics", Comput. Methods Appl. Mech. Engrg., 192, 975-1016, 2003. doi:10.1016/S0045-7825(02)00435-8

3

M. Kegl, B. Brank, "Shape optimization of truss-stiffened shell structures with variable thickness", Comput. Methods Appl. Mech. Engrg., 195, 2611-2634, 2006. doi:10.1016/j.cma.2005.05.020

4

J. Korelc, "Symbolic methods in numerical analysis", www.fgg.uni-lj.si/symech

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)