Keywords: initial equilibrium problem, catenary, cable structures, railway overhead, geometric stiffness.

In high-speed trains the energy supply is obtained through the interaction between the pantograph of the moving vehicle and the overhead catenary system which consists of a cable tension structure. As it is well known tension structures pose the problem of finding the shape of the stressed reference configuration which is called an initial equilibrium problem. The determination of the initial equilibrium problem is an inverse structural problem. Initial equilibrium problems imply that not only the stressed reference configuration must be determined but also the internal stress distribution. When the finite element method is used to solve the initial equilibrium problem some redefinition of the geometry of the mesh from one iteration to another, in order to find the relationship between both geometries, is required. Considering the structural properties of cables the problem exhibits a highly nonlinear behaviour leading most of the cases to convergence problems. Moreover, as many authors have pointed out, see for instance [1], one of the most important drawbacks of dynamic simulation of catenary-pantograph interaction is the resulting dependency on the initial conditions. Conventional modelling by means of the finite element technique exhibits well known problems such as pour robustness, remeshing and geometry redefinition or low convergence rate. Consequently, the determination of the mesh of the initial equilibrium problem increases substantially the computational cost.

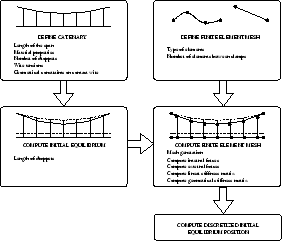
The goal of the article is to apply the method presented in [2] to define a finite element mesh of the initial equilibrium problem of the railway overhead. In Figure 1 a sketch of the method proposed herein is shown and it can be summarized as follows. Defining the geometry, material properties, external forces and geometrical constraint on the contact wire, the initial equilibrium problem is solved using the algorithm described in the paper. Once the initial equilibrium is solved, the position and the internal forces at each point of the cable structure are known. Then, specifying the type and number of elements the mesh is defined. Finally, solving the resulting system of nonlinear equations the discretized initial equilibrium problem is determined.

The accuracy and robustness of the method are inherited from the analytical description used. The method has been applied to determine directly the finite element mesh of the initial equilibrium problem of railway overheads. This finite element mesh is the initial condition to solve the dynamic simulation of the catenary-pantograph interaction. The method presented herein provides accurate and robust initial equilibrium conditions which can be readily plugged into other numerical methods. Despite this method has been applied to simple catenary overheads, other topologies such as stitched or compound catenaries are easily included in the formulation. Moreover, the method can be applied to any vertical planar cable structure.

1

M. Arnold and B. Simeon. Pantograph and catenary dynamics: a benchmark problem and its numerical solution. Applied Numerical Mathematics, 34(4):345-362, 2000. doi:10.1016/S0168-9274(99)00038-0

2

O. Lopez-Garcia, A. Carnicero, and V. Torres. Computational of the initial equilibrium of railway overheads based on the catenary equations. Engineering Structures, In press, 2006. doi:10.1016/j.engstruct.2006.01.007

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)