
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Pre-Stressed Roof Networks with Different Contour Structures
1Department of Transportation,
2Department of Structural Design,
Tallinn University of Technology, Estonia
An orthogonal hypar-network consists of concave carrying and convex stretching cables and may be described as a translatory surface:
| (13) |
In case of vertical loading, the condition of equilibrium may be written in form:
| (14) |
(2) Using also equations of deformation compatibility and Galyorkin [3] procedure, we obtain system of equations for relative deflections of the network and for the cable forces. An approximate analysis of a hypar-network brings us to a cubic equation for determination of the network's relative deflection:
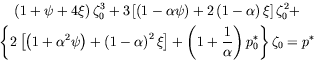 |
(15) |
In discrete analysis, generally a system of vector equations is to be solved [4,5]. In case of orthogonal cable network structures, the condition of equilibrium is to be formed for every node:
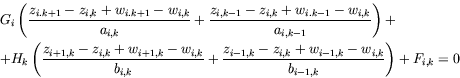 |
(16) |
and equations of deformations compatibility for every cable:
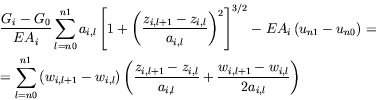 |
(17) |
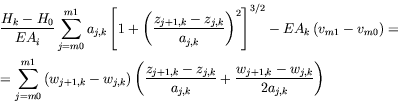 |
(18) |
For contour beam we can use any computational method, such as the finite element method, which give
us deformations, depending of cable forces ![]() and
and ![]() . Solving the system of
equations give us all node deformations, cable forces and internal forces in contour
beam. Using this method we get more possibilities to use different load
combinations, different contour beams and cable networks, but simultaneously we
obtain a large non-linear equations system that is difficult to solve.
. Solving the system of
equations give us all node deformations, cable forces and internal forces in contour
beam. Using this method we get more possibilities to use different load
combinations, different contour beams and cable networks, but simultaneously we
obtain a large non-linear equations system that is difficult to solve.
For the numerical example, a hypar-network with main parameters ![]() m,
m, ![]() m,
m,
![]() m and an analogical network surrounded by two inclined arches were chosen for
detailed analysis [5]. Comparison of the behaviour of cable networks with different
contour beams are presented in the paper.
m and an analogical network surrounded by two inclined arches were chosen for
detailed analysis [5]. Comparison of the behaviour of cable networks with different
contour beams are presented in the paper.
- 1
- H.A. Buchholdt, "An Introduction to Cable Roof Structures", Thomas Telford, London, 1999
- 2
- I. Tärno, "Effects of contour ellipticity upon structural behaviour of hyparform suspended roofs", Publ. of Royal Institute of Technology, Stockholm, 1998.
- 3
- B.G. Galyorkin, "Collection of works", Publ. of the USSR Academy of Sciences (in Russian)
- 4
- V. Kulbach, "Statical analysis of girder- or cable-stiffened suspended structures", Proc. Estonian Acad. Sci., Eng., 1, 2-19, 1995.
- 5
- V. Kulbach, J. Idnurm, I. Talvik, "Analysis of saddle-shaped cable networks with different contour structures", Proc. Estonian Acad. Sci., Eng., 2, 101-114, 2002
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)