engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Eigenmotions of a One Degree of Freedom Viscoelastically Damped System
Laboratory of Modelling, Materials and Structures (LM2S), University Pierre and Marie Curie, Paris, France
| (8) |
the search of eigensolutions in the form
For a system with ![]() DOFs with classical viscous damping, Bulatovic [3] has
given conditions for the
DOFs with classical viscous damping, Bulatovic [3] has
given conditions for the ![]() eigenmotions to be all damped with oscillations (so-called heavily
damped systems).
eigenmotions to be all damped with oscillations (so-called heavily
damped systems).
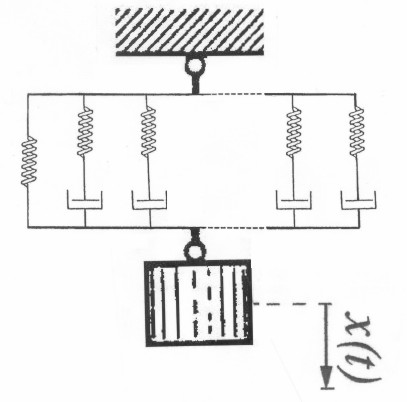
Systems with ![]() DOF with a viscoelastic spring, the rheology of which is
represented by a so-called three parameters model, have been studied by Muller [4].
DOF with a viscoelastic spring, the rheology of which is
represented by a so-called three parameters model, have been studied by Muller [4].
For a system with ![]() DOF
DOF ![]() consisting of a mass
consisting of a mass ![]() associated with a
viscoelastic spring with relaxation modulus
associated with a
viscoelastic spring with relaxation modulus ![]() , the governing equation is:
, the governing equation is:
| (9) |
and the search of eigensolutions in the form
where
When this viscoelastic spring is represented by a Biot's model with ![]() parameters
the relaxation modulus takes the form of a so-called "Prony's series":
parameters
the relaxation modulus takes the form of a so-called "Prony's series":
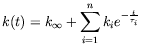 |
(11) |
where the relaxation times
The Laplace-Carson transform of ![]() may then be written in the form:
may then be written in the form:
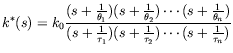 |
(12) |
where
- 1
- S. Adhikari, Eigenrelations for Nonviscously Damped Systems, A.I.A.A. Journal, 39, 8, 2001, 1624-1630. doi:10.2514/2.1490
- 2
- S. Adhikari, Dynamics of Nonviscously Damped Linear Systems, J. Engng Mech., 2002, 328-339. doi:10.1061/(ASCE)0733-9399(2002)128:3(328)
- 3
- R.M. Bulatovic, On the Heavily Damped Response in Viscously Damped Dynamic Systems, J. Appl. Mech., 71, 2004, 131-134.doi:10.1115/1.1629108
- 4
- P. Muller, Are the Eigensolutions of a 1-d.o.f. system with Viscoelastic Damping Oscillatory or not?, J. of Sound and Vibration, 285, 2005, 501-509. doi:10.1016/j.jsv.2004.09.007
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)