Keywords: uncertainty quantification, adaptive estimation, stochastic systems, polynomial chaos, stochastic Galerkin methods.

Many models in science and engineering involve some element of uncertainty. If this uncertainty is modelled with probabilistic methods, one has to consider systems with uncertain or random parameters. The main interest here is with random fields, which model the spatial variability of random parameters.

A simple stationary model of groundwater flow may illustrate this [4]:

where is the hydraulic head, the random conductivity, f and random sinks and sources, and the spatial domain, and a probability space with probability measure .

Discretisation in space is performed by the finite element method, and various techniques exist to take account of the random nature of the governing equation [3]. The stochastic variability may also be treated with Galerkin methods [2,4]. The solution is a stochastic field--in tensor product form . A variational formulation is [4]: Find , such that (with appropriate spatial Sobolev spaces and spaces of random functions ):

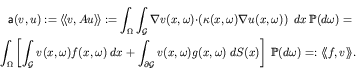
Following the "Galerkin recipe", one takes finite dimensional subspaces of , using the Karhunen-Loève expansion (KLE) of the random field and Wiener's polynomial chaos expansion (PCE) as a stochastic ansatz, the discrete form of the problem then looks like [4]:

Here is the (block)-vector of polynomial chaos coefficients of the solution, represents the sinks and sources, are very similar to usual stiffness matrices, come from the KLE of the conductivity , and are produced by the PCE, where is a multi-index to designate the PCE functions.

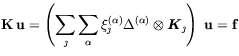
Often a functional of the solution is the main point of interest; in this case the solution process can be used to estimate the error of the approximated value , where is the continuous representation of the discrete solution given by , and this estimate can be used to adaptively steer the computation [1]. For simplicity assume that the functional is linear, as well as its approximation , then the error in the functional can be estimated simply by adjoint techniques. View the linear functional as , then , and the dual solution may be interpreted as a sensitivity.

The error in the functional is 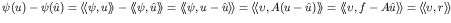, where is the residuum, which gives these techniques the name of dual weighted residual methods (DWRM). The dual solution is in practice also only computed approximately, giving , and the error estimate becomes . For the adaptive steering, we want to know whether to include a certain basis function in the Galerkin ansatz or not. For the stochastic part, do the following [1,2]: When coarsening, i.e. throwing out a basis vector, look at the inner product of the residuum with the projection of the sensitivity onto that basis vector b. If this is very small in absolute value, that basis vector is thrown out. To check whether to include a new basis vector, just the projection of the residual onto the basis vector is computed, if this is sufficiently large, that basis vector is used in the computation of . In this way a small but efficient (low error for the functional ) basis can be found in an adaptive manner.

1

A. Keese, H.G. Matthies, "Adaptivity and sensitivity for stochastic problems." In P. Spanos, G. Deodatis (eds.), "Computational Stochastic Mechanics 4", pp. 311-316, Millpress, Rotterdam, 2003.

2

A. Keese, Numerical Solution of Systems with Stochastic Uncertainties : A General Purpose Framework for Stochastic Finite Elements. Doctoral thesis, Technische Universität Braunschweig, Brunswick, 2004. URL

3

H.G. Matthies, C.E. Brenner, C.G. Bucher and C. Guedes Soares, Uncertainties in Probabilistic Numerical Analysis of Structures and Solids--Stochastic Finite Elements, Structural Safety, 19, 283-336, 1997. doi:10.1016/S0167-4730(97)00013-1

4

H.G. Matthies, A. Keese, Galerkin methods for linear and nonlinear elliptic stochastic partial differential equations, Comp. Meth. Appl. Mech. Engrng. 194, 1295-1331, 2005. doi:10.1016/j.cma.2004.05.027

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)