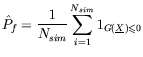Keywords: uncertainties, probability, FORM, reliability, Monte Carlo simulations, sensitivity factor, retaining wall.

When designing a civil engineering structure, the designer deals with various sources of uncertainties. The principal ones are physical uncertainties, materials properties, geometrical characteristics, loads, statistical uncertainties associated with the random variables, and mechanical model uncertainties [1]. The probabilistic methods are therefore very helpful in order to evaluate the structural sensitivity to the randomness of the whole parameters that may be involved. In the present study, a cantilever soil retaining wall is analyzed and its probability of structural failure is investigated.

The probabilistic approach is based on a mechanical model, in which the structural parameters are considered as random variables . The failure mechanism of the structure is described by a limit state function . The failure probability of the structure is then expressed [2].

A reliability analysis and a sensitivity study are performed. Two kinds of probabilistic approaches are considered: a FORM method as well as Monte Carlo simulations.

In the first order reliability methods, the limit state function is approximated by a hyper-plane in the vicinity of the design point [1,2]. When the partial derivates of the limit state function are not available analytically, many geometrical methods might be run. The "rotating planes method" based on a cyclic relaxation method is used in this paper [3].

The Monte Carlo simulation [4], transforms equation (2), as the expectation of the function , and its estimate [5], is given by

where is the number of simulations and if and else.

In order to accelerate the Monte Carlo convergence, importance and conditioning techniques are used herein [5].

Three failure mechanisms are considered for the retaining wall: overturning, sliding and ultimate bearing and the mechanical models considered are those commonly used in engineering practice [6]:

• Rankine or Coulomb theory in order to evaluate the active soil pressure
• Vésic, Hansen or Meyerhof methods in order to evaluate the bearing capacity

In this present study, it appears that some of the variables have a dominant effect for the whole failure modes that are considered. Furthermore, in this particular case, the model used to evaluate the active pressure does not greatly affect the reliability index or the failure probability. But, the structural reliability is greatly influenced by the mechanical model for the bearing capacity. Moreover, there is a great similarity between the three failure methods that have been considered. The Monte Carlo method with conditioning and importance sampling gives larger failure probabilities than the FORM method.

1

A. Ang, W.H. Tang, "Probability Concepts in Engineering Planning and Design", J.Wiley et Sons, New York, 1984

2

R.E. Melchers, "Structural reliability analysis and prediction", Ellis Horwood, 1999.

3

A. Mébarki, M. Lorrain, "Algorithmes pour l'analyse de la fiabilité par la méthode de l'hypercône et le calcul de l'index de sécurité BETA", Annales des Ponts

4

R.Y. Rubinstein, "Simulation and the Monte Carlo Method", John Wiley & Sons, Inc., 1981. doi:10.1002/9780470316511

5

A. Sellier, A. Mébarki, "Importance zone and Importance Sampling in Reliability Analysis of Civil Structures", International Journal of Pressure Vessels and Piping, Elsevier Sc. Publishers, vol. 61, 1995.

6

Naval Facilities Engineering Command, "Foundations & Earth Structures", Alexandria, Virginia 22332-2300.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)