In order to include the warping behavior in the study of the aforementioned element in each node at the element ends a seventh degree of freedom is added to the well known six DOFs of the classical three-dimensional frame element. The additional DOF is the first derivative of the angle of twist dd denoting the rate of change of the angle of twist , which can be regarded as the torsional curvature of the cross section.

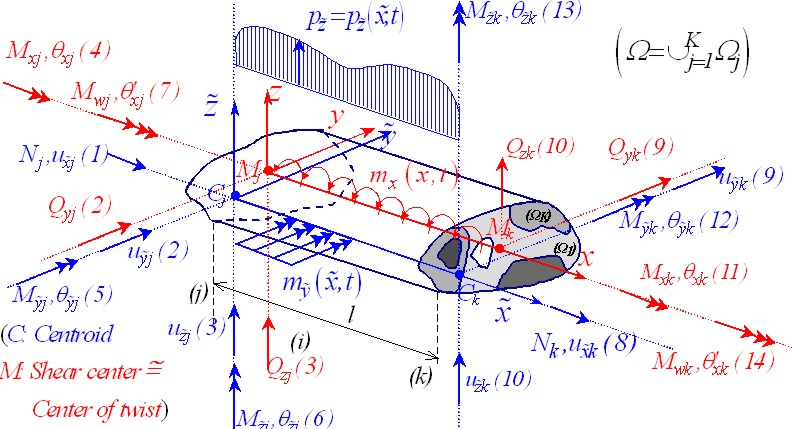
For the solution of the problem at hand, a boundary element method is developed for the construction of the stiffness matrix and the nodal load vector, of a member of an arbitrarily composite cross section, taking into account both warping and shear deformation effects, which together with the corresponding mass and damping matrices lead to the formulation of the equation of motion. The composite member consists of materials in contact each of which can surround a finite number of inclusions. To account for shear deformations, the concept of shear deformation coefficients is used. In this investigation the definition of these factors is accomplished using a strain energy approach [1], instead of Timoshenko's and Cowper's definitions, for which several authors have pointed out that one obtains unsatisfactory results or definitions given by other researchers, for which these factors take negative values. Eight boundary value problems with respect to the variable along the bar angle of twist, to the primary warping function, to a fictitious function, to the beam transverse and longitudinal displacements and to two stress functions are formulated and solved employing a pure BEM approach [2], that is only boundary discretization is used. Both free and forced transverse, longitudinal or torsional vibrations are considered, taking also into account effects of transverse, longitudinal, rotatory, torsional and warping inertia and damping resistance. Numerical examples are presented to illustrate the method and demonstrate its efficiency and accuracy. The influence of the warping effect, especially in composite members of open form cross section is analyzed through examples demonstrating the importance of the inclusion of the warping degrees of freedom in the dynamic analysis of a space frame. Moreover, the discrepancy in the dynamic analysis of a member of a spatial structure arising from the ignorance of the shear deformation effect necessitates the inclusion of this additional effect, especially in thick walled cross section members.

Figure 1: Prismatic beam of an arbitrarily shaped composite cross section.

1

V.G. Mokos, E.J. Sapountzakis, "A BEM Solution to Transverse Shear Loading of Composite Beams", Int. J. Solids Structures, 42, 3261-3287, 2005. doi:10.1016/j.ijsolstr.2004.11.005

2

E.J. Sapountzakis, "Torsional Vibrations of Composite Bars by BEM", Composite Structures, 70, 229-239, 2005. doi:10.1016/j.compstruct.2004.08.031

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)