
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
A Three-Dimensional Hybrid Finite Element for Singular Stress Analysis in Composite Structures
1Laboratoire de Génie et Matériaux Textiles, Roubaix, France
2Laboratoire de Mécanique de Lille, UMR CNRS 8107, Villeneuve d'Ascq, France
|
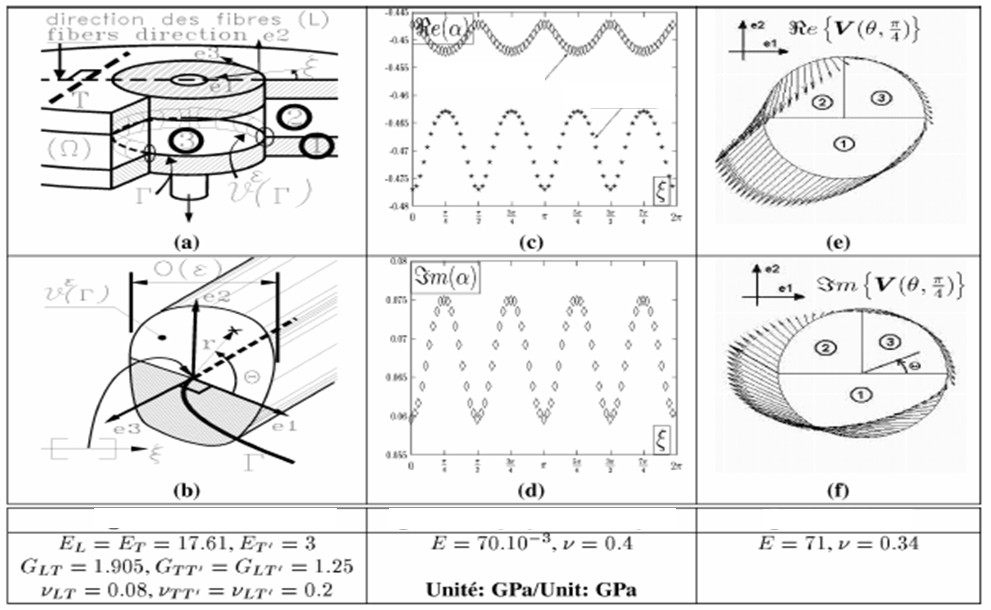
Let ![]() be the angular parameter along a junction line (or a crack front),
be the angular parameter along a junction line (or a crack front), ![]() and
and ![]() be
the polar coordinates in the current plane orthogonal to the junction line (or the
crack front). In the curvilinear coordinate system
be
the polar coordinates in the current plane orthogonal to the junction line (or the
crack front). In the curvilinear coordinate system
![]() , the asymptotic singular part
of the stress field near the junction line has the following form [1,2]:
, the asymptotic singular part
of the stress field near the junction line has the following form [1,2]:
| (1) |
The complex number a is the singularity exponent. Unlike for cracks in
homogeneous materials, it is not generally equal to -1/2. The determination of its
value is a first numerical difficulty to face. This computation already gives
qualitative information, helpful to the design. This requires considering an
eigenvalue problem in complex variable. A numerical algorithm was successfully
implemented for solving it and obtaining the eigenstress field ![]() .
.
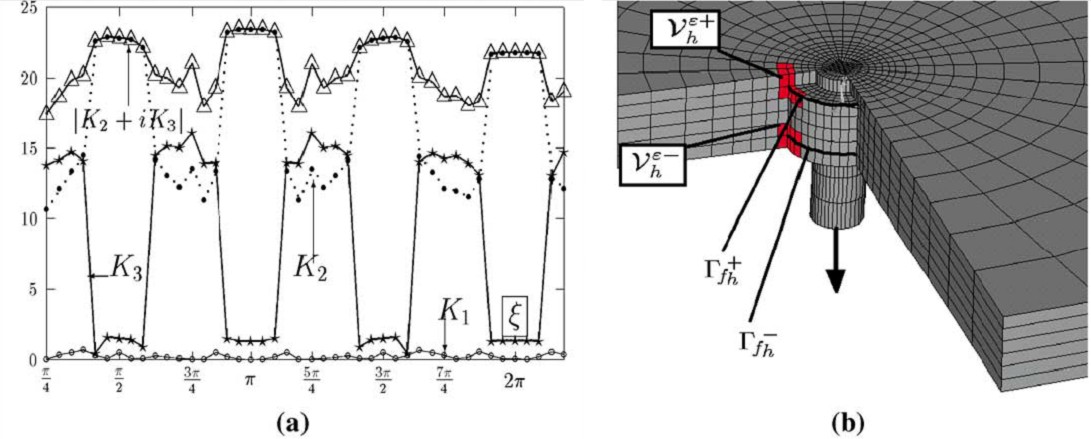
Next, accurate values of the associated stress intensity factors ![]() are computed. We
implemented a 3D mongrel hybrid finite element, based on a unisolvent
displacement field and an equilibrated stress field enhanced by the previously
determined singular field. The Babuška-Brezzi inf-sup condition enables the selection the
appropriate stress mode functions [3], as highlighted by a benchmark. The approach
is illustrated for the previous sandwich-insert junction in Figure 2.
are computed. We
implemented a 3D mongrel hybrid finite element, based on a unisolvent
displacement field and an equilibrated stress field enhanced by the previously
determined singular field. The Babuška-Brezzi inf-sup condition enables the selection the
appropriate stress mode functions [3], as highlighted by a benchmark. The approach
is illustrated for the previous sandwich-insert junction in Figure 2.
|
- 1
- S.G. Lekhnitskii, "Theory of Elasticity of an Anisotropic Body", Holden-Day, San Francisco, USA, 1963.
- 2
- D. Leguillon, É. Sanchez-Palencia, "Computation of Singular Solutions in Elliptic Problems and Elasticity", Masson, Paris, France, 1987.
- 3
- T.H.H. Pian, D. Chen, "On the suppression of zero energy deformation modes", International Journal of Numerical Methods in Engineering, 19, 1743-1752, 1983. doi:10.1002/nme.1620191202
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)