Keywords: elastic stiffened plate, reinforced plate with beams, bending, ribbed plate, analog equation method.

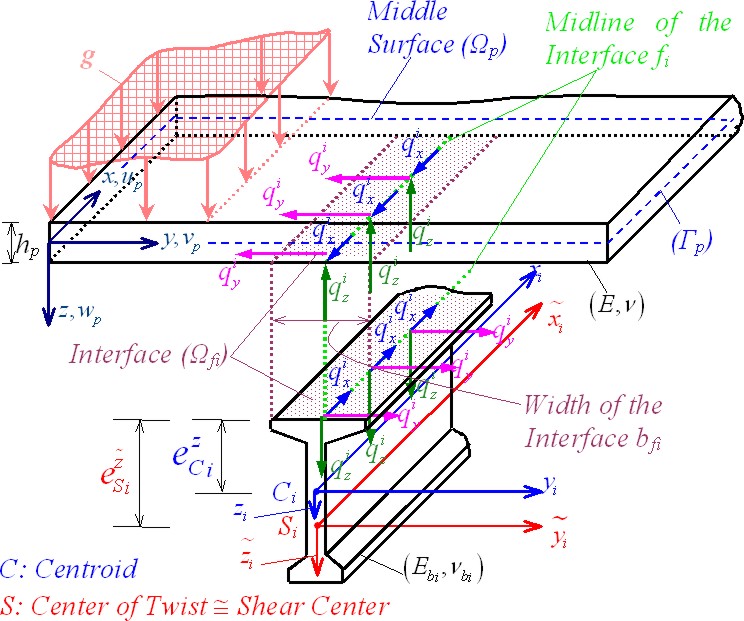
A general solution for the analysis of plates stiffened by arbitrarily placed non-intersecting beams of arbitrary cross section is presented. The adopted structural model is a refined one of that proposed by Sapountzakis and Katsikadelis in [1]. According to this model, the stiffening beams are isolated from the plate by sections in the lower outer surface of the plate, taking into account the arising tractions in all directions at the fictitious interfaces (Figure 1). The aforementioned integrated tractions result in the loading of the beams as well as the additional loading of the plate. Their distribution is established applying continuity conditions in all directions at the interfaces. Six boundary value problems with respect to the plate transverse deflection, to the plate inplane displacement components, to the beam transverse deflections, to the beam axial deformation and to the beam nonuniform angle of twist are formulated and solved using the analog equation method (AEM), a BEM based method employing a boundary integral equation approach [2]. The solution of the aforementioned plate and beam problems, which are nonlinearly coupled, is achieved using iterative numerical methods. The essential features and novel aspects of the present formulation compared with previous ones are summarized as follows.

i.

The stiffened plate is subjected to an arbitrary loading, while both the number and the placement of the nonintersecting stiffening beams are also arbitrary (eccentric beams are also included).

ii.

The influence of the transverse traction component at plate-beams interfaces is taken into account. Thus, the adopted model permits the evaluation of the transverse inplane shear forces at the interfaces between the plate and the beams, the knowledge of which is very important in the design of prefabricated plate beams structures (estimation of shear connectors in the transverse direction).

iii.

Displacement continuity conditions at the interfaces are applied along all three axes of the coordinate system, leading to the formulation of a system of equations involving two nonlinear functions, namely the longitudinal and transverse inplane shear forces at the interfaces.

iv.

The cross section of the stiffening beams is an arbitrary one. Thereby, the eccentricities of both the centroid and the shear center axes with respect to the midline of the plate - beam interface are also included.

v.

The nonuniform torsion in which the stiffening beams are subjected is taken into account by solving the corresponding problem and by comprehending the twisting and warping arising in the corresponding displacement continuity conditions.

vi.

Terms arising from the internal variable axial loading of both the plate and the beams coming from the longitudinal and transverse inplane shear forces at the interfaces are taken into account.

The adopted model better describes the actual response of the plate beam system and permits the evaluation of the shear forces at the interfaces in both directions, the knowledge of which is very important in the design of prefabricated ribbed plates.

1

E.J. Sapountzakis, J.T. Katsikadelis, "Analysis of Plates Reinforced with Beams", Computational Mechanics, Vol.26, 66-74, 2000. doi:10.1007/s004660000156

2

J.T. Katsikadelis, "The Analog Equation Method. A Boundary - only Integral Equation Method for Nonlinear Static and Dynamic Problems in General Bodies", Theoretical and Applied Mechanics, 27, 13-38, 2002.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)