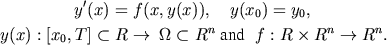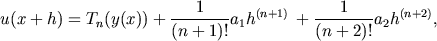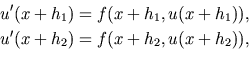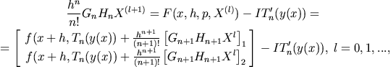Keywords: implicit Taylor series methods, numerical methods, initial values problems, collocation methods, parallel algorithms, piecewise polynomials.

In this paper we give implicit generalization of several explicit Taylor series methods. This generalization means, that the classical truncated Taylor series we extend with extra terms and the unknown coefficients in these extra terms we determine by several collocation conditions. These collocation conditions give the implicit extension of the methods.

The main idea of the rehabilitation of the Taylor series algorithms is based on the new possibility to calculate formally the truncated Taylor series as approximate solutions, but approximate calculation of higher derivatives using well-known technique for the partial differential equations gives more chance to use this old technique [1].

We regard the following ordinary differential equation initial value problem (ODE IVP).

We suppose, that the solution of the problem has continuous derivatives up to order , where is a desired number, . Its value depends on the order of truncated Taylor series order we want use in the construction. Let be the approximate solution of the problem (18). We look for it in truncated Taylor series form with extra terms.

where and are unknowns to be determined an is the -th order truncation Taylor series of exact solution. The conditions to determine the unknown values and are the following collocation conditions.

where and are not equal fixed stepsize (they can have both positive and negative values). The equations (20) is nonlinear algebraic system of equations for the unknown values and .

In the paper we show that the following theorem is valid. If the solution of the problem (18) has solution , than the method defined by (19) and (30) is an asymptotically order method and the approximate solution (19) gives a -th order approximation of the exact solution in some neigbourhood of .

The algorithm given by (19) and (20) is a collocation type implicit algorith for the solution of ODE initial value problems. We describe a symple iteration algorithm for the solution for one step of the implicit method.

Let us introduce the following notation:

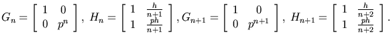Using these notations the system of equations (20) defining the suggested numerical algorithm can be rewrited into the following form:

where denotes the -th component of the vector, is the unit matrix and this equation defines the vector function.

We prove if the function for has a continuous derivative, then the algebraic equation arising from (19) and (20) for small enough has a unique solution and this solution can be determined by simple iteration.

1

P.E. Miletics, G. Molnárka, "Taylor Series Methods with Numerical Derivatives", Hungarian Electronic Journal of Sciences, ser. Applied and Numerical Mathematics, pp. 1-15, 2002.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £95 +P&P)