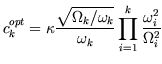Keywords: viscous damper, vibration control, passive damping, flexible structure, spray boom, mast structure.

A simple methodology is developed to install viscous dampers on flexible structures with low inherent damping in order to reduce vibrations. Approximating formulas are derived for the maximum attainable modal damping and corresponding optimal damping constant at a given damper location. The potential and the limitations of the methodology are demonstrated by two case studies: damping of agricultural spray boom structures and damping of mast structures.

Incorporating viscous dampers in flexible structures can be a very effective means of reducing unwanted vibrations. In doing so, two questions have to be answered: where are the dampers placed in the structure; and what are the optimal damping constants resulting in minimized vibrations?

In the literature usually very complex algorithms are used to optimize damping constants, according to either an eigenvalue-based criterium or an energy criterium, starting from a discrete representation of the structure by its mass and stiffness matrix [1,2]. The damper position is rarely incorporated in the optimization procedure [3], despite the fact that this position is most critical.

In this paper it is shown that finding a good damper location and optimal damping constant can be very easy in the case one single viscous damper is used to optimize the modal damping of one particular eigenmode. Simple approximating formulas are derived for the maximum attainable modal damping of the eigenmode and the corresponding optimal damping constant at a given damper location

and

where are the resonance frequencies of the structure, are the resonance frequencies of the structure with locked damper, and is the static stiffness of the structure at the damper location. These parameters are easily obtainable from a model of the structure constructed with commercial finite element software and they are also easily experimentally identifiable.

The approximation is only valid when the eigenmodes of the structure are not significantly changed by locking the damper, which is for example the case when a relative damper is placed in a structure, or when an absolute damper is attached near the anchorage of a stay cable or near the clamping point of a mast structure. This is verified by numerical simulations and experiments in the two case studies: damping of agricultural spray booms and damping of mast structures.

1

S.J. Cox, I. Nakic, A. Rittmann, K. Veselic, "Lyapunov optimization of a damped system", Systems & Control Letters, 53, 187-194, 2004. doi:10.1016/j.sysconle.2004.04.004

2

K. Veselic, K. Brabender, K. Delinic, "Passive control of linear systems", M. Rogina, et al., (Eds), Applied Mathematics and Computation, Department of Math, University of Zagreb, Zagreb, 39-68, 2001.

3

M. Gürggöze, P.C. Müller, "Optimal Positioning of Dampers in Multi-body Systems", Journal of Sound and Vibration, 158(3), 517-530, 1992. doi:10.1016/0022-460X(92)90422-T

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)