Keywords: concrete, cracking, nonlinearity, smeared fixed crack model, triangular layered plate element.

This paper is concerned with the computational modelling of reinforced concrete slabs. It develops a 3-node, 18-DOF triangular layered plate element for the geometric and nonlinear analysis of reinforced concrete plates and shells at service load levels. The proposed element combines a 3-node, 9-DOF triangular membrane element with drilling freedoms, and a refined, non-conforming 3-node, 9-DOF triangular plate bending element to account for the coupling between membrane and bending actions. While a large number of layered triangular and quadrilateral elements have been reported in the literature for the finite element (FE) analysis of plates and shells, the majority possess some undesirable features in their formulation and in their implementation. The proposed element here is simple and efficient, and it is underpinned by Allman's well-known triangular membrane element with drilling degrees of freedom [1], and the RT9 element developed by Cheung and Cheng [2].

The inclusion of the drilling degrees of freedom makes the incorporation of the element into other commercial software packages relatively simple, and avoids common singularities that occur in flat plate and panel analysis. Because of the application of the refined non-conforming element RT9, displacement continuity conditions along the element boundaries are satisfied in an average sense, the relevant convergence criteria are satisfied, and the performance of the element is robust.

A powerful feature of the numerical procedure is its treatment of concrete nonlinearity by easily-implemented constitutive models. When the maximum principal stress at a Gauss point reaches the concrete tensile strength, cracks form in planes perpendicular to the direction of the maximum principal stress, with the elastic properties reducing to zero in the maximum principal stress direction. When the minimum principal stress also reaches the tensile strength, a second crack plane perpendicular to the first one forms, and an appropriate property matrix is deployed. The shear modulus used in this property matrix accounts for aggregate interlock and dowel action, and is based on the formulation of Cedolin and Deipoli [3]. Tension-stiffening effects are also included, according to the model of Izumo et al. [4].

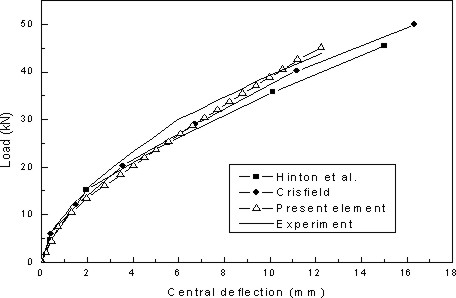
The paper presents some calibration studies against experimental results, including the modelling of Dudeck's slab [5] shown in Figure 172.1. This, and other studies, show consistency of the proposed element with other numerical treatments, and with experimental results reported elsewhere.

1

D.J. Allman, "A Compatible Triangular Element Including Vertex Rotations for Plane Elasticity Analysis", Computers and Structures, 19, 1-8, 1984. doi:10.1016/0045-7949(84)90197-4

2

Y.K. Cheung, W.J. Chen, "Refined Nine-Parameter Triangular Thin Plate Bending Element by using Direct Stiffness Method", International Journal for Numerical Methods in Engineering, 38, 283-298, 1995. doi:10.1002/nme.1620380208

3

L. Cedolin, S. Deipoli, "Finite Element Studies of Shear-Critical R/C Beams", Journal of the Engineering Mechanics Division, ASCE, 103(EM3), 395-410, 1977.

4

J. Izumo, H. Shin, K. Meakawa, H. Okamura, "An Analytical Model for PC Panels Subjected to In-Plane Stresses", Concrete Shear in Earthquakes. Elsevier Applied Science, London, 206-215, 1992.

5

H. Duddeck, G. Griebenou, G. Schaper, "Material and Time-Dependent Non-Linear Behaviour of Cracked Reinforced Concrete Slabs - Finite Element Analysis and Laboratory Tests", in Non-Linear Behaviour of Reinforced Concrete Spatial Structures, Preliminary Report 1, G. Mehlhorn et al. (eds), Werner, Düsseldorf, Germany, 101-113, 1978.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)