Computational Technology Resources - CCP

Keywords: traffic flow, cellular automata, stochastic velocity model, metastable phenomenon.

Summary

Introduction

This paper describes the traffic flow simulation using cellular automata.

Some researchers have presented several cellular automata models for traffic flow simulations. However, most of the existing studies focus to the traffic flows on the freeways. When the freeway traffic models are applied to the urban city traffic flows, there are some problems due to intersections, traffic signals and so on. To avoid the problem, the simulation model using the velocity representation defined by stochastic variable is described in this study. The final goal of our study is to develop the simulation model for the traffic flow in urban cities. However, in this paper, the present algorithm is applied to two-lane freeway traffic flows in order to compare the results by the present scheme with the actual data.

Local Rules

Cellular automata simulations are performed according to local rules. Local rules of the present scheme are composed of the behavior and velocity local rules.

Definition of behavior local rules depend on the problem to be simulated. In the present scheme, basic local rules for going-ahead and lane-changing of cars are defined in advance and then, exact definition of the rules are re-defined for the problems.

The velocity local rules are defined as follows.

Acceleration:

If $v < v_{\max}$ and $GAP > GAP_{safe}$ then, $v \to v_{\max}(P+\alpha)$ .

Decelaration:

If $GAP < GAP_{safe}$ then, $v \to v_{\max}(P-\alpha)$
where $v, v_{\max}, GAP_{safe}$ and $\alpha$ denote the present velocity, the feasible maximum velocity, the safety car distance and the acceleration of a car, respectively. The safety car distance $GAP_{safe}$ is calculated from the velocity v according to Japanese automobile inspection certification manual.

Numerical Examples

A two-lane freeway is considered as the object under consideration. Each road is defined as a queue of 1000 cells. At an initial iteration step, cars are placed according to regularized random numbers at the average of 0.06 and the standard deviation of 0.03. Cars move to rightward direction. Since cyclic boundary conditions are specified at the ends of the roads, cars passing at right end come into the domain from the left end. As a result, the car density in the domain is kept invariant during the simulation. Simulation parameters are specified as; cell size is 3m width by 3m length, feasible maximum velocity is 80Km/h, minimum safety car distance is 30m.

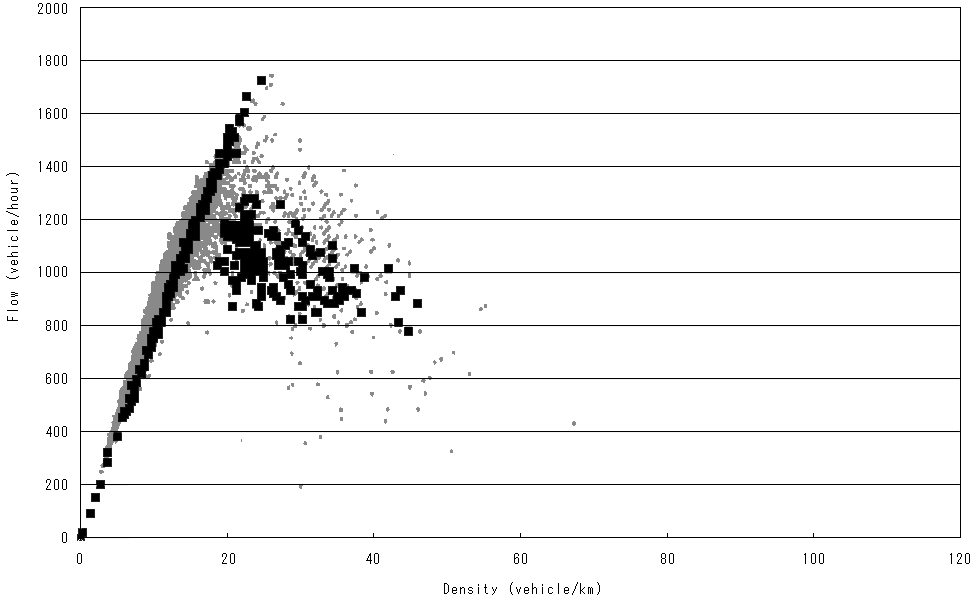
Numerical results are shown in Figure 66.1. The abscissa and the ordinate denote traffic density (number of cars for 1km) and traffic volume (number of cars passing thought the road for each hour), respectively. Gray and black dots indicate actual and simulated results, respectively. Actual data are estimated from the traffic flow between Toyota and Okazaki in Tomei expressway in Japan in August 1999. The actual and simulated data show the discontinuity of traffic volume at the traffic densities between 20 and 30. The discontinuity is named as metastability or metastable phenomenon. We can notice that the metastable phenomenon is represented well in computer simulation.

**Figure 66.1:** Traffic flow and density

Acknowledgment

This work has been supported by Foundation of Toyota Rikagaku Kenkyusho.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £82 +P&P)