Keywords: Schwedler domes, design, neural networks, radial basis functions, back propagation.

Space structures are often used for covering large spans. Sport stadiums, assembly halls, exhibition centers, swimming pools, shopping arcades and industrial buildings are typical examples of structures where large unobstructed areas are essential and where minimum interference from internal support is required. Space structures are often classified as grids, domes and barrel vaults [1].

Configuration processing and data generation for space structures can be simplified using the concepts from formex algebra [2]. For preprocessing and for efficient solutions, theory of graphs can be employed. Though an optimal analysis can be carried out using usual matrix displacement method, however, for large-scale problems, the analysis is usually time consuming due to a large number of equations being involved [3]. Therefore approximate methods are beneficial in the process of nonlinear analysis and optimal design.

Neural networks provide a powerful tool for approximate analysis and design of space structures. Such networks are trained using backpropagation [4] and counterpropagation networks [5,6], among many others.

In the present paper, efficient neural networks are trained for prediction of the displacements and design and of Schwedler domes using NeuralWorks software [7]. Single layer domes with varying the spans between 42.5 and 65 meters, with an increment of 2.5 meters, are considered. Radial Basis Functions (RBF) and Backpropagation (BP) networks are employed for training and testing these nets. For accurate distribution of the applied forces and wind load on the nodal points, additional programs are developed. Analysis and design are carried out employing ANSYS software for preparing the training and testing pairs.

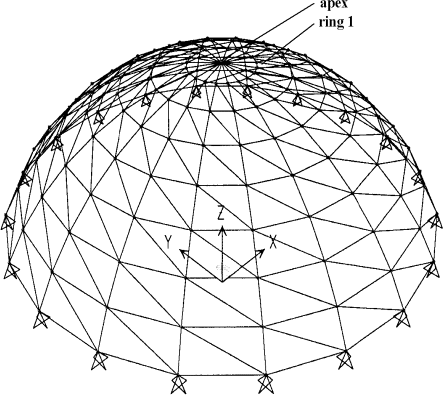
The model selected for the study of this paper is a single layer Schwedler dome with ribbed members are considered as beam elements joined together rigidly and diagonal members are taken as bar elements, Figure 62.1. The spans are varied between 42.5m and 65m with the steps of 2.5 meters. The opening angle of the domes is chosen from the angles between 45 and 67.5 degrees. A typical Schwedler dome used in this study is shown in Figure 62.1(a). Simple supports are considered for the exterior ring of the dome. The number of intervals between the ribs is considered as 20 and for rings this number is taken as 8.

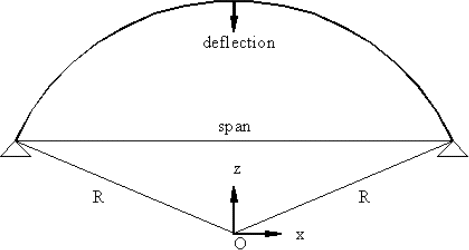
In order to simplify the design, and due to symmetry, 8 types of cross sections are considered for the members of a typical rib. The span and deflection at the apex of the dome are illustrated in Figure 62.1(b).

1

Makowski, Z.S., Analysis, Design and Construction of Braced Schwedler domes, Nichols Pub. Co., New York, 1984.

2

Nooshin H., Disney P. and Yamamoto C., Formian, Multi-Science Publishing Company, UK, 1993.

3

Kaveh A., Optimal Structural Analysis, Research Studies Press (John Wiley), UK, 1997.

4

Kaveh, A. and M. Raeissi Dehkordi, "BP and RBF Neural Networks for the Analysis and Design of ribbed domes", International Journal of Space Structures, accepted for publication, 2003. doi:10.1260/026635103322437463

5

Hajela P. and Berke L., "Neurobiological computational models in structural analysis and design", Computers and Structures, 41(1991)657-667. doi:10.1016/0045-7949(91)90178-O

6

Iranmanesh A. and Kaveh A., "Structural optimisation by gradient base neural networks", International Journal of Numerical Methods in Engineering, 46(1999)297-311. doi:10.1002/(SICI)1097-0207(19990920)46:2<297::AID-NME679>3.3.CO;2-3

7

NeuralWare, Using NeuralWorks, NeuralWare, USA, 1993.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £82 +P&P)