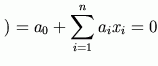engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE NINTH INTERNATIONAL CONFERENCE ON CIVIL AND STRUCTURAL ENGINEERING COMPUTING
Numerical Estimation of Sensitivities for Complex Probabilistically-Described Systems
Centre for Infrastructure Performance and Reliability, The University of Newcastle, Australia
The performance is the expectation over a (preferably large) number of sample performances:
where
For system optimization or design refinement, it is helpful to have available the
sensitivity of
![]() X
X![]() to (small) changes in X and hence to (small) changes in the
parameters v. When
to (small) changes in X and hence to (small) changes in the
parameters v. When
![]() X
X![]() is not explicit, that is, there are no known analytical
expressions for (any or all) the performance function(s), Monte Carlo simulation
employing crude finite differences is the most common method for sensitivity
estimation. It is computationally very demanding.
is not explicit, that is, there are no known analytical
expressions for (any or all) the performance function(s), Monte Carlo simulation
employing crude finite differences is the most common method for sensitivity
estimation. It is computationally very demanding.
The approach proposed herein to estimate the gradients and sensitivities at the
point of maximum likelihood x*
and to construct a 'response surface'
![]() X
X![]() to
approximate the actual performance function. This may then be used to estimate the
gradients and sensitivities. Such a surface may be constructed from the some or all
of the realizations (samples) from a Monte Carlo analysis used to estimate Equation (120.1):
to
approximate the actual performance function. This may then be used to estimate the
gradients and sensitivities. Such a surface may be constructed from the some or all
of the realizations (samples) from a Monte Carlo analysis used to estimate Equation (120.1):
that is, the 'expected' system performance
where
The gradients (e.g.
![]() , etc.) are obtained from the direction cosines to the
hyper-plane obtained from the coefficients
, etc.) are obtained from the direction cosines to the
hyper-plane obtained from the coefficients ![]() . For parameter sensitivities only the
mean and standard deviation are considered (e.g.
. For parameter sensitivities only the
mean and standard deviation are considered (e.g.
![]() etc. and
etc. and
![]() etc.). A
robust if unsophisticated approach is to use the tangent hyper-plane and finite
differences based on the results from the (one) Monte Carlo analysis.
etc.). A
robust if unsophisticated approach is to use the tangent hyper-plane and finite
differences based on the results from the (one) Monte Carlo analysis.
When there are constraint functions
G![]() x
x![]() ,
,
![]() on the values x may
assume and if
x* falls in the inadmissible space
G
on the values x may
assume and if
x* falls in the inadmissible space
G![]() x
x![]() ,
,
![]() , the formulation
is slightly modified. Typically, there will be one or more points
x*j,
, the formulation
is slightly modified. Typically, there will be one or more points
x*j,
![]() but usually only one will be of interest.
but usually only one will be of interest.
One example is given to illustrate that the approximate technique produces results for gradient and for sensitivities very close to the theoretical results. The second example shows how the gradients and sensitivities change with changes in the constraint equation. The change in behaviour is smooth, indicating a gradual change in sensitivity as the boundary moves. However, when the boundary reaches the point of maximum likelihood for the unconstrained performance function the gradients are then uninfluenced by a change in location of the constraint. There are corresponding jump changes in parameter sensitivities. The reason for this is discussed.
The examples illustrate that the proposed technique produces satisfactory results even for highly nonlinear performance functions, implying very considerable approximations in the use of a tangent hyperplane. Importantly, the results for gradients and sensitivities were obtained without repeated Monte Carlo simulation runs. The proposed technique requires little computational effort beyond that required for the original Monte Carlo simulation.
It was found that the proposed technique provided a satisfactory approach for estimating gradients and parameter sensitivities for a number of highly non-linear performance functions, including some with constraints on admissible regions.
- 1
- Melchers R.E. and Ahammed M. (2002) Gradient estimation for applied Monte Carlo analyses, Reliability Engineering and System Safety, 78(3) 283-288. doi:10.1016/S0951-8320(02)00172-2
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £123 +P&P)
![$\displaystyle )] = \int L($](cc03/img247.gif) X
X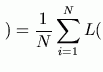 X
X