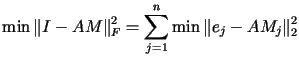Keywords: preconditioning, approximate inverses, minimal residual algorithm, threshold dropping strategies, sparse linear systems, GMRES algorithm.

We now consider the linear system of equations

where the coefficient matrix is a large, sparse, and nonsymmetric. In general, the convergence of iterative algorithm is not guaranteed or may be tremendously slow. Therefore, the original system of equations (44.1) has to be transformed into more well mannered form. To do so, we consider the preconditioned system

where is a preconditioner and should be chosen a good approximate right-inverse matrix for . As the primary goal is to reduce the total execution time, both the computation of the preconditioner and the matrix-vector product should be evaluated in parallel mode.

In recent papers, it has been shown that the direct computation of sparse approximate inverses leads to appropriate preconditioners in parallel environment. The starting point is the minimization problem

for a given sparsity pattern of the matrix , and is the identity matrix. This minimization problem (44.3) is inadequately parallel. If we allow only a few non-zero entries in the -th column of , then the equation (44.3) reduces to the solution of small least squares problems

These procedures have originally been developed for fixed sparsity pattern of . However, in many cases, it is not possible to find a good and sparse a priori pattern for . Thus, it is necessary to drop smaller entries in in the course of the iteration process.

We will analyze another way to determine previously a suitable pattern for . The minimal residual (MR) algorithm for computing a sparse approximate inverse of coefficient matrix is investigated, and it is very useful for deriving an explicit preconditioner in restarted GMRES() algorithm, especially in a parallel environment. We present MR algorithm in Figure 44.1. Starting with the zero vector as an initial estimation for , an iterative method, which is called minimal residual (MR) algorithm, is applied for solving the problem (44.4). Then automatically, the column vector gets more and more dense, and in order to retain the sparsity of , it is necessary to drop smaller entries in in the course of the iteration process. Explicitly, a drop tolerance droptol is introduced to compute approximate inverse . We now propose the approximate inverse procedure whose name calls MR(lfil, droptol, ) algorithm, where lfil is the maximum number of entries per column and is a parameter of stopping criterion for MR iterations. In the restarted GMRES() method, the Krylov basis vectors are kept sparse by dropping entries just after the self-preconditioning step, before the multiplication by . Dealing with which entries are drop, we can develop a dual threshold strategy droptol and lfil.

Numerical experiments are given for solving the discretized problems (44.1) derived from the boundary value problems of PDE (partial differential equation) on the shared memory parallel machine Origin 2400 with 8 processors. For instance, several numerical results of two dimensional convection diffusion problems will be reported in our presentation. We also present both from a theoretical and a practical point of view that the preconditioner created by MR algorithm is useful in improving the convergence of restarted GMRES() algorithm.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £85 +P&P)