Keywords: nonlinear analysis, reinforced concrete, stress integration, cross-section analysis, Gauss-Legendre quadrature, biaxial bending.

This paper deals with the implementation of a modified integration procedure for arbitrary geometry reinforced concrete cross sections with axial forces and biaxial bending, from service load to ultimate load. The proposed method is applicable in sections which stress field is uniform at least in one direction. The method decompose the integration area in thick layers parallel to the most tensile stressed fibre, which definition depends on the constitutive equation of the concrete. The integration of the stress field of each thick layer is transformed into a path integral over the perimeter of this layer, evaluating them by the Gauss-Legendre cuadrature. The fundamentals of the method are explained in the paper and different possibilities for this purpose are analysed. The obtained results for the different alternatives are compared in accuracy and in speed in relation with the results obtained with the classical fibre decomposition method, Mari [1], and also with other methods proposed by same authors, Miguel et al. [2] and Bonet et al. [3] and a recently method proposed by Fafitis [4]. In the study among the four analysed methods (Cells, Fafitis, "Thick Layers Integration" and "Modified Thick Layers Integration"), applied in different concrete section types, the following conclusions are achieved:

a)

In all the cases, with the same runtime, the accuracy of the gaussian integration methods is notably higher than the fibre method.

b)

The accuracy of the gaussian integration methods is higher as many number of Gauss points are used, except in the method proposed by Fafitis. The accuracy level of this method depends on the form of the function used to represent the concrete stress-strain relationship.

c)

The accuracy level of the fibre decomposition method does not depend only on the mesh density but also in its adaptation to the geometry to the section.

d)

Due to the form that adopts the concrete constitutive equation defined by the Model-Code 90 which (depends on the strength), the accuracy level is reduced as the strength of concrete is increased for all the integration methods.

e)

Both, the "TLI" (Thick Layer Integration) and "MTLI" (Modified Thick Layer Integration) method show an excellent accuracy level (lower than 0.02%) for a 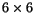Gauss mesh points per quadrilateral or 6 Gauss points per side of the perimeter that forms the thick layer.

f)

When the accuracy level and the runtime for the three gaussian methods are compared with the fibre decomposition method, it is observed that the "MTLI" method is more efficient, followed by the "TLI" method and the last one is the Fafitis' method.

g)

The efficiency of the "MTLI" method is confirmed in the integration of high strength concrete sections (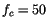MPa).

Finally, the proposed "modified thick layers" method (MTLI), regarding the accuracy, efficiency, and continuity in the stress field integration it is advisable for the implementation in nonlinear reinforced concrete frameworks programs.

1

Mari, A.R.: "Nonlinear geometric, material and time dependent analysis of three dimensional reinforced and pretressed concrete frames", Report No. USB/SESM-84/12, Departament of Civil Engineering, University of California, Berkley, California, USA, June 1984

2

Miguel, Pedro F.; Bonet, José L.; Fernández, Miguel A.: "Integración de tensiones en secciones de hormigón sometidas a flexocompresion esviada", Revista Internacional de Métodos Numéricos para el cálculo y diseño en ingenieria, V.16, No 2, pp 209-225, 2000. (in spanish).

3

Bonet, J.L; Miguel, P.F.; Fernández, M.A.; Romero, M.L.: "Efficient Procedure for Stress Integration in Concrete Sections Using a Gauss- Legendre Cuadrature", Proceedings of the Eighth International Conference on Civil and Structural Engineering Computing, B.H.V. Topping, (Editor), Civil-Comp Press, Stirling, United Kingdom, paper 53, 2001. doi:10.4203/ccp.73.53

4

Fafitis, A.: "Interaction Surfaces of Reinforced-Concrete Sections in Biaxial Bending", Journal of Structural Engineering, ASCE, Vol. 127, No 7, July, 2001, pp 840-846. doi:10.1061/(ASCE)0733-9445(2001)127:7(840)

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)