Keywords: multilayered plates, refined theories, mixed methods, finite element, zig-zag, interlaminar continuity, transverse normal stress.

Multilayered made structures are increasingly used in aerospace, ships, automotive vehicles, advanced optical mirrors and semiconductor technologies. In most of the applications, these structures mostly appear as flat (plates) or curved panels (shells). In this work, attention has been restricted to flat geometries, although most of the presented derivations and techniques could be extended to shell cases. The analysis of multilayered, anisotropic structures is difficult when compared to one layered ones made of traditional isotropic materials. A number of complicating effects arise when their mechanical behavior as well as failure mechanisms have to be correctly understood. As far as two dimensional modeling is concerned, the subject to which this paper is devoted, layered structures also require special attention. This is due to the intrinsic discontinuity of the thermo-mechanical properties at each layer-interface to which high shear and normal transverse deformabilty is associated. An accurate description of the stress and strain fields of these structures requires theories that are able to describe the so-called Zig-Zag (ZZ) form of displacement fields in the thicknes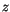s -direction as well as Interlaminar Continuous (IC) transverse shear and normal stresses. These two facts have been summarized in [1] as 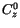-Requirements, that is displacements and transverse stress components must be 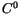function in the thickness direction 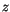. Transverse and in-plane anisotropy of multilayered structures along with the fulfillment of the 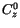-Requirements make it difficult to solve practical problems related to layered structures. The use of both refined two-dimensional theories and computational methods become mandatory to solve practical problems related to multilayered structures. Among the several available computational methods, the Finite Element Method (FEM) has played and continues to play a significant role. Most of the commercial codes that are used in small and large companies as well as in Research Centers are, in fact, finite element oriented.
A large number of refined theories and computational strategies have been proposed and implemented over the last four decades. Many review works are available on these subject. Among these, recommended reviews are those quoted in the articles [2,3]. The subjected of the present work is that of multilayered finite elements that are able to furnish an accurate description of strain/stress fields in multilayer flat structure analysis. Recent author's findings [1], [2],[5] are herein employed to formulate in unified manner a large variety of finite elements. Reissner's Variational Mixed Theorem, RMVT, and Principle of Virtual Displacements, PVD, have been used to derive advanced(*) and classical multilayered finite elements, respectively. The number of both the order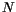 of expansion in 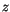and the number of nodes 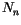of the elements, are taken as free parameters of the considered RMVT and PVD formulations. Layer stiffness are accumulated at plate as well as layer level by permitting than Equivalent Single Layer, ESLM, as well as Layer-Wise, LW, variable description.
In order to lower the number of the equations related to the several presented finite elements as much as possible, an indicial notation has been used. As a fundamental property such an indicial notation has led to the writing of all the finite element matrices in terms of a few arrays, which are called fundamental nuclei, the dimension of which is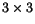 . These fundamental nuclei are herein written at a layer level; such a choice has permitted to the author to treat both modelings which preserve the number of variables independent of the number of layers (Equivalent Single Layer Models, ESLM) and Layer Wise Models (LWM) in which the same variables are independent in each layer, at the same time. The variational statements and continuity requirements for stresses and displacements as well as non homogeneous boundary conditions at each interface, for displacement and/or transverse stress variables, are used to derive matrices from layers to multi-layers and from elements to structure levels.
A numerical investigation has been proposed to assess and compare the implemented finite elements. Numerical results and discussion have been provided in the extended version of this work.

1

Carrera E.,"A class of Two Dimensional Theories for Multilayered Plates Analysis", Atti Accademia delle Scienze di Torino, Mem Sci. Fis., 19-20, 49-87, 1995

2

Carrera E., "Developments, Ideas and Evaluations based upon the Reissner's Mixed Theorem in the Modeling of Multilayered Plates and Shells", Applied Mechanics Review , 54, 301-329, 2001. doi:10.1115/1.1385512

3

Reddy J N, "Mechanics of Laminated Composite Plates, Theory and Analysis". CRC Press, 1997

4

Idlbi A, Karama M and Touratier M, "Comparison of various laminated plate theories ", Composite Structures , 37, 173-184, 1997. doi:10.1016/S0263-8223(97)80010-4

5

Carrera E., Demasi L., "Classical and Advanced Multilayered Plate Elements based upon PVD and RMVT. Part I. Derivation of Finite Element Matrices, doi:10.1002/nme.492; Part II. Numerical Implementations", doi:10.1002/nme.493; IJNME , in press

Footnotes

... advanced*

The use of the word advanced has been preferred by the authors, over few others, such as `refined', `mixed' or `higher order'.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)