
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE SIXTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Numerical Solution by Energy Minimization of Hyperelastic Membrane in Large Displacements and Finite Strains
Laboratoire de Génie Civil de Nantes Saint-Nazaire, Faculty of Science and Technology, University of Nantes, France
In this paper, the membrane structures are solved by directly minimizing the total potential energy. Although theoretically equivalent to the traditional finite element method, the proposed approach proves to be a more robust and efficient technique. All the numerical computations are performed using a three-dimensional flexible triangular finite element, which is able to handle the abovementioned non-linearities. The finite element has no bending stiffness and the tangent matrix is singular for the rotation degrees of freedom. The numerical solution is carried out by means of an iterative method like the conjugate gradient or Newton one.
The strain energy is given by a quasi-incompressible hyperelastic potential density in the reference configuration written in the following form:
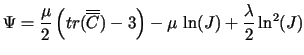 |
(84.1) |
First, the proposed finite element is validated through the well-known Hencky problem [1] which consists of the inflation of a circular membrane clamped at the rim. For this problem we recall the analytical solution in the case of isotropic linear elastic behavior [2,3], before the comparison between the analytical solution and the finite element results. Next, an extension to a nonlinear hyperelastic behavior is treated, which allows us to exhibit the pressure value which leads to the material instability of the circular membrane.
The second application is related to problem of an orthotropic rectangular membrane. We focus on two points: first we present a semi-analytical solution in the case of orthotropic linear behavior for the rectangular membrane. Then, this solution is used to validate once again the finite element in the case of isotropic behavior.
- 1
- H. Hencky, "On the Stress State in Circular Plates With Vanishing Bending Stiffness", Zeitschrift f�r Mathematik und Physik, 63, 311-317, 1915.
- 2
- W.B. Fichter, "Some solutions for the large deflections of uniformly loaded circular membranes", NASA Technical Paper 3658-NASA Langley Research Center, Hampton, VA, 1997.
- 3
- J.D. Campbell, "On the theory of initially tensioned circular membranes subjected to uniform pressure", Quart J. Mech. & Appl. Math., Vol IC, Pt 1, 84-93, 1956.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)