Keywords: constitutive equations, energy conjugate stresses, hyper-elastic.

The concept of energy conjugacy first presented by Hill [1] states that a stress measure is said to be conjugate to a strain measure if represents power or rate of change of internal energy per unit reference volume. Based on this definition, Guo and Man [2] derived explicit tensorial formulations for conjugate stress for , while earlier, the stress measure conjugate to logarithmic strain tensor , had been derived by Hoger [3]. Also, following the Hill's principal axis method and energy conjugacy notion, a relation between the components of two Seth-Hill conjugate stress tensors in the principal axes was derived in [10]. Some well known relations of the Seth-Hill strain measures with their conjugate stresses are givien in [5,6,7]. Also basic relations were derived for the rate of logarithmic strain [4].

Use of hypo-elastic constitutive equations for large strains in nonlinear finite element applications usually needs special considerations [8]. For example, the strain doesn't vanish in some elastic loading and unloading closed cycles, and they need objective rate tensors, and incrementally objective algorithm for numerical application and integration. Some of them may fluctuate under excessive shear deformation [8]. Hyper-elastic constitutive equation in comparison, don't need these considerations. However, their behaviour for large elastic strains is important, and may differ in tension and compression. In the present work, Hyper-elastic constitutive equations for the Seth-Hill strains and their conjugate stresses are explored as a natural generalisation of Hook's law for finite elastic deformations. Based on the uniaxial and simple shear tests, the response of the material for different constitutive equations is examined. Some required kinematic and tensor equations are used from [6,10]. Together with an objective rate model, the effect of different constitutive laws on Cauchy stress components is compared. It is shown that the logarithmic strain and its conjugate stress give answers closer to that of the rate model. In addition, use of Biot stress-strain pairs for a bar element, results in an elastic spring which obeys the hook's law even for large deformations and behaves the same in tension and compression. The volume change of material is another factor which is noticed.

1

R. Hill, "On constitutive inequalities for simple materials", Int. J. Mech. Phys. Solids, 16, 229-242, 1968. doi:10.1016/0022-5096(68)90031-8

2

Z.-H. Guo, C.-S. Man, "Conjugate stress and tensor equation 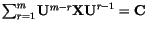", International Journal of Solids and Structures 29 (16), 2063-2076, 1992. doi:10.1016/0020-7683(92)90194-X

3

A. Hoger, "The stress conjugate to logarithmic strain", Int. Journal of Solids and Structures, 23 (12), 1645-1656, 1987. doi:10.1016/0020-7683(87)90115-6

4

M.E. Gurtin, K. Spear, "On the relationship between the logarithmic strain rate and the stretching tensor", Int. Journal of Solids and Structures 19, 437-444, 1983. doi:10.1016/0020-7683(83)90054-9

5

R.W. Ogden, "Nonlinear elastic deformations", Ellis Harwood, 1984.

6

Z.-H. Guo, R.N. Dubey, "Basic aspects of Hill's method in solid mechanics", SM Arch, 9, 353-380, 1984.

7

R. Hill, "Aspects of invariance in solid mechanics", Advances in Applied Mechanics 18, 1-75, 1978. doi:10.1016/S0065-2156(08)70264-3

8

J.K. Dienes, "On the Analysis of Rotation and Stress Rate in Deforming Bodies", Acta Mechanica, 32, 217-232, 1979. doi:10.1007/BF01379008

9

A. Hoger, D.E. Carlson, "Determination of stretch and rotation in the polar decomposition of deformation gradient", Quart. App. Math. 10, 1984.

10

K. Farahani, R. Naghdabadi, "Conjugate stresses of the Seth-Hill strain tensors", International Journal of Solids and Structures, 37, 5247-5255, 2000. doi:10.1016/S0020-7683(99)00209-7

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)