Large eigenvalue problems arise in many scientific and engineering problems. While the basic mathematical ideas are independent of the size of matrices, the numerical determination of eigenvalues and eigenvectors becomes more complicated as the dimensions and the sparsity of matrices increase. Special methods are needed for efficient solution of such problems.

Methods are developed for decomposing the graph models of structures in order to calculate the eigenvalues of matrices with special patterns, ref. [1]. The eigenvectors corresponding to such patterns are studied in ref. [2]. In this paper, graph models are associated with dynamic systems.

Decomposition approaches are employed to form matrices of special patterns for such systems. The problem of finding eigenvalues and eigenvectors of symmetric dynamic systems is transferred into calculating those of their subsystems.

In this article an symmetric matrix is considered with all entries being real. For three special forms, the eigenvalues of are obtained using the properties of its submatrices.

Form I -

In this case 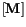has the following pattern:

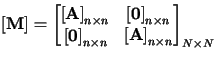
with .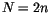

Form II -

For this case matrix 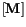can be decomposed into the following form:

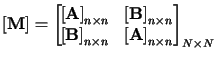
Form III -

This form has a Form II submatrix augmented by some rows and columns as shown in the following:

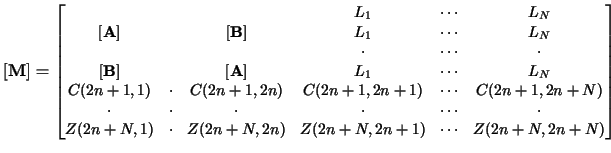Where is a matrix, with a submatrix with the pattern of Form II, and augmented columns and rows. The entries of the augmented columns are the same in each column, and all the entries of are real numbers.

In is concluded that: symmetry in dynamic systems results in the decomposition of the systems into smaller subsystems called the vibrating cores. The matrices corresponding to these cores have smaller dimensions and contain part of the properties of the vibrating system.

Symmetry of a mathematical model corresponds to the symmetric distribution of the physical properties comprising of masses and stiffnesses of the springs and the connectivity of the masses by means of springs.

For the graph model of a dynamic system, symmetry of Form II results in two vibrating cores C and D. These cores are physically identified with the difference of C being more flexible than D, and the main frequency and the corresponding mode in this part of the model. The core C is in fact half of the system in one side of the symmetric axis and its property contains the properties of the whole system.

If the graph model of a vibrating system has Form III symmetry, then two vibrating cores D and E will be produced. The number of masses and springs in D are less than E and in the core E directed springs are included.

1

Kaveh, A. and Sayarinejad, M.A., "Eigenvalues for matrices of special patterns using graph symmetry", Scientia Iranica, accepted for publication, 2002.

2

Kaveh, A. and Sayarinejad, M.A., "Eigensolutions for matrices of special patterns", Communs Numer. Meths Engng, In press, 2002. doi:10.1002/cnm.656

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)