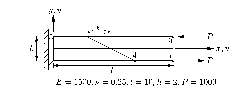Keywords: traction free, finite element, assumed stress, drilling degrees of freedom.

This paper investigates new methodologies for the accurate representation of traction free sides using membrane finite elements with drilling degrees of freedom and an assumed stress interpolation.

Firstly, a method based on direct enforcement of the traction free condition through manipulation of the assumed stress field of an element is presented (e.g. see Xiao et al. [1]). Secondly, a penalty-equilibrated approach, in which stress equilibrium is enforced in individual elements, is presented (e.g. see Wu and Cheung [2]). In the penalty-equilibrated approach, weak enforcement of equilibrium is proposed herein, in which the stress derivatives are modified as to alleviate locking-like behavior.

The methodologies are applied to the families of assumed stress membrane finite elements with drilling degrees of freedom recently proposed by Geyer and Groenwold [3], for which the potential energy is given by

This formulation results in three independent interpolation fields arising from the translations, rotations and the stress assumption. Rather conventional, the stress field is constructed as     , resulting in the and families presented by Geyer and Groenwold. However, in both families for irregular geometries, is not optimal. This makes these elements susceptible to loss of accuracy as a result of element distortions. This lack of robustness may mostly be overcome using the techniques already mentioned in the preamble, and which are briefly summarized in the following sections.

Direct enforcement of the traction free condition: Writing the traction free condition under consideration as , we select a primary trial stress field for as a complete second order polynomial. Substitution of the traction free condition into at , which describes the traction-free side, then yields an optimal interpolation matrix . exactly satisfies the stress condition on the traction free side. The resultant element has 12 parameters, and is denoted HB12.

Penalty equilibrated version of the element: Ignoring the effect of distributed loads within elements, element equilibrium is written as

where represents the 2-D differential operator. Using matrix notation, the potential energy of the elements under consideration becomes

with     , and

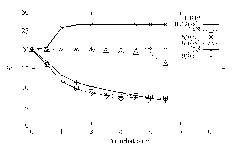
Four elements are formulated, namely HB12, , and . All the elements pass the patch test, are rank sufficient and invariant. When applied to the pure bending problem depicted in Figure 22.1, we note that the and elements developed are highly accurate, as is graphically depicted in Figure 22.1.

1

Q.Z. Xiao, B.L. Karihaloo, and F.W. Williams. Application of penalty-equilibrium hybrid stress element method to crack problems. Engng. Fract. Mech., 63:1-22, 1999. doi:10.1016/S0013-7944(99)00015-6

2

C.-C. Wu and Y.K. Cheung. On optimization approaches of hybrid stress elements. J. Finite Elem. Anal. Des., 21:111-128, 1995. doi:10.1016/0168-874X(95)00023-0

3

S. Geyer and A.A. Groenwold. Two hybrid stress membrane finite element families with drilling rotations. Int. J. Num. Meth. Eng., 53:583-601, 2002. doi:10.1002/nme.287

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)