
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE SIXTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Area Integral of a Stress Function over a Beam Cross-Section
Department of Structural Mechanics, Faculty of Civil Engineering, Czech Technical University in Prague, Czech Republic
Imagine a given plane of deformation
We can obtain exact analytical expressions for the cross-section internal forces. The constitutive stress-strain function are usually expressed as a continuous function by parts polynomial. Such functions can be easily integrated in a closed form and therefore we get (3.2), (3.3), (3.4) without any hard work.
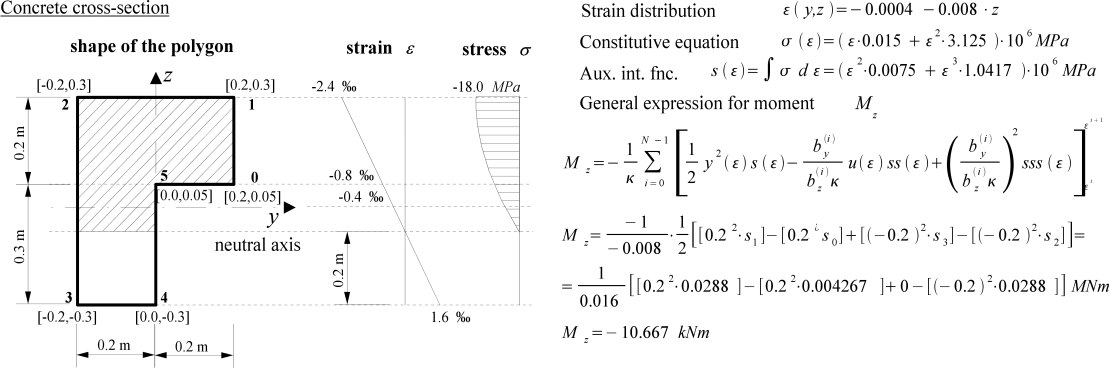
For illustration of the process we present here a simple example. The concrete L
shaped cross-section is described with an irregular polygon. The constitutive stress-
strain function is
![]() MPa.
From an affiliated analysis
we obtain linearly distributed strain
MPa.
From an affiliated analysis
we obtain linearly distributed strain
![]() .
The task is to
compute the corresponding internal forces quickly and accurately. In this example
we limit us only to a bending moment
.
The task is to
compute the corresponding internal forces quickly and accurately. In this example
we limit us only to a bending moment ![]() and use derived integral expressions to
evaluate the resultant.
and use derived integral expressions to
evaluate the resultant.
The presented path integration of non-linearly distributed stress over the cross- section is a very powerful computational method. This method is extremely useful for the concrete reinforcement design and assessment, especially due to its algorithmic efficiency. The method enables us to operate with cross sections of different shapes and materials. The runtime of the integration is determined by the complexity of the defined cross section shape. This means that we can model any arbitrary shape of cross-section that can be approximated with a line polygon without any restrictions as for orthogonality or orientation. Nevertheless, if we work with a simple rectangular cross section loaded in the direction of its symmetry plane, we obtain as efficient expression of the integration of stress function as possible.
- 1
- R. Vondrácek, "Numerical methods in nonlinear concrete design", Master's thesis, Czech Technical University in Prague 2001.
- 2
- Z. Bittnar, J. Sejnoha, "Numerical methods in structural mechanics I-II", ES CVUT, Prague 1992
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)
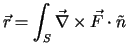 d
d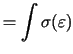 d
d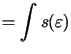 d
d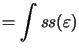 d
d