Keywords: piles, closed-form solutions, lateral loading, soil-structure interaction.

Closed-form solutions for laterally loaded piles have been established recently, accounting for various head and base conditions. The solutions are based on load transfer approach by simplifying the pile-soil interaction as independent springs along the pile shaft and at the pile base. The key of the approach is the determination of the subgrade modulus for the springs. Although a few expressions originally developed for beam analysis were used for the determination, the usage has not been rigorously verified. In this paper, the rationality of the usage has been examined in comparison with various numerical results available. Particularly the accuracy and sufficiency of the load transfer approach and the coupling effect has been explored in detail. Rigorous expressions for lateral pile analysis, and the determination of subgrade modulus, and the coupling effect are provided.

A number of simple solutions were developed for laterally loaded piles using an empirical load transfer ( curve) model [1] or a 2-parameter model [2]. The load transfer model treats the soil along the shaft and at the base as independent elastic springs. The validity of the models essentially depends on the estimation of the (1-D) properties of the elastic springs, which are able to represent the 3-D response of the surrounding soil.

The modulus for the springs was obtained through fitting with relevant rigorous numerical solutions [3,4]. The problem is that the fitting to different reactions (e.g. deflection or moment of a beam or a pile) generally leads to different values of modulus. This difference in modulus implies that the uncoupled model is not sufficiently accurate for simulating the pile-soil interaction. The available experiments demonstrate that the displacement field around a laterally loaded pile is significantly different from that around a beam sitting on an elastic medium [5,6]. Unfortunately, rigorous guidelines about the estimation of the modulus are not available for lateral piles.

Recently, a new model was developed [7], which is based on both an assumed displacement pattern and a rational stress field, and is represented through two parameters: modulus of subgrade reaction, for the independent springs, and a fictitious tension of a stretched membrane used to tie together the springs. The new model maintains the features, and circumvents the instability problem at high Poisson's ratio of the 2-parameter model. With the new model, new closed-from solutions were generated in a compact form for various pile-head and base conditions. The values of and the were generated for various cases using variational principle. The solutions compare well with various numerical analyses and the available solutions for rigid piles.

In this paper, with the new closed form solutions for lateral piles, the adequacy of using the available expressions [2,3,4,7] for modulus of subgrade reaction has been explored, in comparison with various numerical solutions. The comparison demonstrates that

• The previously available expressions for 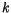are not suitable for pile analysis, particularly for rigid piles, although the suggestion [6] of doubling the value by Vesic [3] sometimes gives a good prediction for flexible piles.
• Generally, using the second parameter 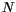is essential and sufficient for lateral pile analysis. Except that in the case of free-head pile due to moment loading only, the second parameter may be ignored. In other words, the conventional `Winkler model' is only sufficiently accurate for the latter case.
• It seems that only with the currently propose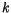d and 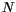, a consistent prediction of pile response with relevant numerical results is noted at any pile- soil relative stiffness.

The results from this research should be useful for both academia and practical engineers.

1

H. Matlock, L.C. Reese, "Generalized solutions for laterally loaded piles." J. of Soil Mech. and Found. Engrg. Div. 86(5), 63-91, 1960.

2

W.D. Guo, F.H. Lee, "Theoretical load transfer approach for laterally loaded piles", Int. J. Num. & Analy. Methods in Geomechanics, 2001, in press.

3

R.F. Scott, Foundation analysis. Prentice Hall, Englewood Cliffs, N. J. 1981.

4

A. Vesic, "Bending of beams resting on isotropic elastic solid." J. of Engrg. Mech., ASCE, 87(2), 35-53, 1961.

5

T. D. Smith, "Pile horizontal soil modulus values." J. of Geotech. Engrg. Div., ASCE, 113(9), 1040-1044, 1987. doi:10.1061/(ASCE)0733-9410(1987)113:9(1040)

6

Y.V.S.N. Prasad, T.R. Chari, "Lateral Capacity of model rigid piles in cohesionless soils." Soil and Foundations 39 (2), 21-29, 1999.

7

J.E. Bowles, Foundation analysis and design. McGraw-Hill International Editions & Sons, Inc. 502-503, and 935, 1997.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)