Keywords: boundary element method, photoelasticity, stress separation, inverse problem.
The application of computational mechanics techniques to inverse problems has
been receiving increasing attention in various branches of science and engineering.
In solid mechanics it may provide non-destructive evaluation tools which can be
used to identify unknown variables at the surface, such as the stress distribution in a
contact region between contacting bodies.
Photoelastic readings provide information regarding the differences of the
principal stresses and their orientations at interior points. However, it is often
difficult to separate the individual Cartesian stress components from the photoelastic
data The BE technique is an ideal companion to photoelastic analysis since, unlike
the finite element (FE) method, the interior solutions can be represented by
unconnected points rather than discretised elements.
This paper presents an inverse boundary element (BE) technique to reconstruct
the boundary conditions in the unknown regions using photoelastic measurements
taken from the photoelastic isochromatic fringe order and the isoclinic angle at interior
points. The separate individual Cartesian stress components are then obtained using
the forward BE method
The BE approach is based on two integral equations: a surface (boundary) integral
equation relating displacements and tractions on the surface, and an interior integral
equation relating the stresses at the interior points to the surface displacements and
surface tractions. The surface (boundary) integral equation is as follows:
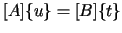 |
(88.1) |
where
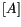
and
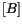
are matrices that contain the numerical integrations involving the
surface kernels. After applying the boundary conditions of the problem, the relevant
elements of the matrices
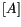
and
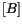
are swapped such that all the unknowns end up
on the left hand side of the equation and the known variables are on the right hand
side, as follows:
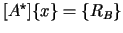 |
(88.2) |
where
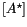
is the solution matrix,
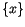
contains all unknown variables (displacements
and tractions), and
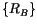
contains all prescribed values of displacements and
tractions. After solving the equations, all tractions and displacements on the
boundary are known. The interior integral equation is as follows:
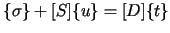 |
(88.3) |
where
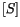
and
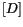
are matrices that contain the numerical integrations involving the
interior kernels. Therefore, in the forward BE approach, the boundary displacements
and tractions are computed first, and then subsequently used to obtain the interior
variables.
The inverse method, as the name implies, uses the interior stress values to
compute the boundary values. By applying the prescribed boundary conditions and
swapping the relevant elements of the matrices
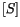
and
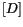
, Equation
88.3 becomes
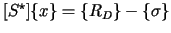 |
(88.4) |
Previous research has shown that inverse BE methods relying on the interior
kernels only cannot be used to obtain the solution, and that it is necessary to use
both interior integral equation
88.4 and surface
integral equation
88.2.
In the unknown region
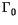
, both the displacements
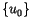
and tractions
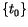
are
unknown. If one set of them is obtained first the remaining unknowns can be solved
as the forward BE procedure. The one which is to be found first will appear on the
right-hand side in equations
88.2 and
88.4 respectively, as follows
Subscript
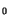
denotes the related partitions belonging to the unknown region
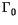
of that
matrix or vector. Combining equations
88.5 and
88.6 and eliminating
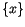
from them,
an equation with
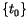
in region
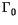
as the only unknowns, can be derived as follows:
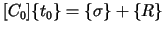 |
(88.7) |
where
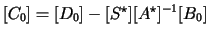 |
(88.8) |
and
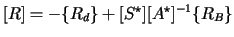 |
(88.9) |
The Singular Value Decomposition (SVD) method is used to solve equation
88.7. It
is clear that once
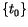
is computed from equation
88.7, the remaining unknowns can
be solved straightforwardly using the forward BE equation
88.5.
The present method to deal with photoelastic stress analysis by employing inverse
BEM described above is to create the interior equations at a number of chosen points
in equation
88.6 by using the difference of Cartesian direct stresses and the magnitude
of the Cartesian shear stress
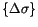
. Accordingly, the coefficients in the matrices
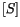
and
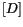
are replaced by
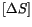
and
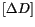
respectively.
This paper also investigates the sensitivity of the inverse BE technique to errors of
photoelastic data at the interior points, discusses how to choose the number and
locations of the interior points and how to improve the numerical algorithm. The
study indicates that the number of measurement points and the location of these
points are important in constructing an accurate system matrix and dealing with the
measurement errors. A criterion for locating the interior measurement points is
given. Examples show good agreement with other solutions even if up to 5% 'noise'
is added to the photoelastic measurement data.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)
