
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON CIVIL AND STRUCTURAL ENGINEERING COMPUTING
Determination of Constitutive Material Parameters for Sheet Metal Forming
The inverse identification procedure is as follows:
Experimental tests are carried out and the data are recorded, e.g. the force- displacement curve. The tests are also simulated using FE-software starting with some chosen material parameters. The material parameters and the friction coefficient are treated as unknowns in the optimization procedure. The objective function is build as a difference between the calculated and the measured punch force formulated in a least square sense. The parameters are then changed using optimization techniques until the objective function reaches a minimum. The values of the parameters at the minimum point are the searched parameters. In case of anisotropy a more complex objective function, which includes also geometric quantities, is implemented.
Two identification problems based on deep drawing experiment are presented. In the first analysis the material is considered to be isotropic. Material parameters are identified using objective function expressed by:
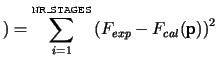 |
(84.1) |
where ![]() is experimentally determined punch force and
is experimentally determined punch force and ![]() is calculated punch force.
The drawing process is divided on
is calculated punch force.
The drawing process is divided on NR_STAGES intervals (stages). In each
stage the punch force is collected from FE software output in order to build up the
objective function. Hollomon's power law [2] was used to describe the plastic
behaviour in this case. The isotropic identification is based on real experiment made
with aluminium 6016-T4. Good agreement between measured and calculated punch
force curves was achieved. Results from inverse based simulations are compared
with simulations based on experimental data achieved from uniaxial tension test
carried out in our laboratory and the friction determined by rotation test taken from
literature[3]. In case of anisotropy the following objective function has been
implemented:
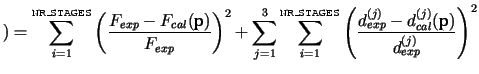 |
(84.2) |
where ![]() is experimentally determined punch force and
is experimentally determined punch force and ![]() is calculated punch
force,
is calculated punch
force,
![]() is experimentally determined flange diameter taken in direction
is experimentally determined flange diameter taken in direction ![]() ,
,
![]() , or
, or ![]() degrees to the rolling direction,
degrees to the rolling direction,
![]() is calculated flange
diameter in direction
is calculated flange
diameter in direction ![]() ,
, ![]() , or
, or ![]() , degrees to the rolling direction.
The index
, degrees to the rolling direction.
The index ![]() is used to distinguish the three applied rolling directions.
The index
is used to distinguish the three applied rolling directions.
The index ![]() is used to distinguish
three applied rolling directions. The drawing process is divided on
is used to distinguish
three applied rolling directions. The drawing process is divided on NR_STAGES
intervals (stages). In each stage the punch force and flange diameters are collected to
build up the objective function. Material behaviour is described by linear hardening
model with Hill's yield criterion[2]. Identification in this case was examined on
artificial data taken from FE simulation. The FE simulation with known material
parameters was used for generation of "experimental" data in this case. Very good
convergence with artificial data was achieved. We are currently working on
coupling this inverse problem with real experiment.
- 1
- Arora, J. S., "Introduction to optimum design", McGraw-Hill Book Company, Singapore, 1989.
- 2
- Hosford W. F., Caddel M.C., "Metal forming", Prentice-Hall, 1993.
- 3
- Benchmark data from "Proceedings of NUMISHEET'99 Volume 2", Eds.: Gekin, J.C., Picart. P., University of Franche-Comte and ENSMM Besancon, France, 1999.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)