
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON CIVIL AND STRUCTURAL ENGINEERING COMPUTING
Optimum Design of Reinforced Concrete Continuous Beams by Genetic Algorithms
Faculty of Engineering, University of Wollongong, Australia
The design of statically indeterminate structures requires the assumption of members' dimensions, followed by analysis of the whole structure, then followed by the design of the members. At the end of this design process, a comparison is made between the initial design and the produced design. If the assumed initial design was smaller than the produced design, then a redesign is necessary. However, if the assumed design was larger than the produced design, then it is up to the designer to make the decision of whether to adopt the initial design or to start again the design process. Each phase of the design/analysis/design cycle is usually lengthy and requires a considerable amount of time and effort. The designer should repeat the process several times in order to obtain a structure that is both safe and economical.
In order to reduce the time and effort involved in the design of economical structures, methods of optimisation have been successfully applied for the last three decades. The success of these methods has been considerable and led to savings both in construction materials and during the design process. However, most such optimisation techniques involve a considerable amount of mathematical formulation and computer programming. In this paper, the optimum design of structures is sought using genetic algorithms. As such, a computer program using Matlab for the optimum design of continuous T and L beams based on genetic algorithms has been developed. The choice of T and L beams was made, as they are not only demanding in analysis but also require a considerable amount of time in design. The problem of optimum design of continuous T and L beams was formulated based on the requirements of the current Australian Standards and the stiffness method is used to analyse the continuous beam. The objective is to minimise the total cost of the beam.
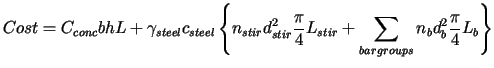 |
(57.1) |
where
Constraints are imposed according to the Australian Standard, AS3600 [1] at each critical location: locations with maximum positive bending moment; negative bending moment and maximum shear force. The following constraints are imposed at each positive bending moment and negative bending moment critical location.
| Flexural strength: |
|
| Minimum reinforcement ratio: |
|
| Spacing: |
|
| Shear strength |
|
- 1
- Australian Standard, "Concrete Structures", Standards Australia, AS 3600, 1994.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)