Keywords: cycle basis, graph theory, frames, force method, semi-rigid joints.

For an efficient force method of frame analysis, special cycle bases should be generated for the formation of localized self-equilibrating systems, leading to sparse flexibility matrices. In this paper, an algorithm is presented using a fundamental cycle basis, where the selected cycles are improved via an algebraic exchange method. Optimal analysis is performed for frames with semi-rigid joints.

In this method, flexibility matrices are generated which are highly sparse (see reference [1,2] for definition). An ordering algorithm is also used for profile reduction to acquire an efficient method for the solution of the corresponding equations.Force method analysis of semi-rigid frames is formulated and a computer code is developed. Examples are analyzed with the present approach and the results are compared to those of SAP 2000.

An efficient algorithm is presented for computing a suboptimal cycle basis of a simple graph . This algorithm is based on the fact that a cycle basis is minimal when no cycle in it can be replaced by a smaller cycle. Fundamental cycle basis of is as input of the algorithm and suboptimal cycle basis is the output. This algorithm exchanges a cycle of a given basis with a smaller one, if possible. Minimum length admissible cycles of can be found by a mapping to an auxiliary graph , and finding specific shortest paths in the  [3]. The procedure of the algorithm is described in the following:

Step 1.

Construct a fundamental cycle basis 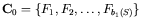as an initial cycle basis.

Step 2.

For 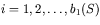find a minimum length cycle 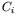in which 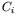is linearly independent o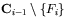f . If 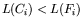, replace 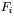by .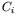

In order to control the independency of a new cycle, one can use the kernel of the cycle-member incidence matrix. The kernel of is required to find out the independency of a new cycle, with respect to the remaining cycles. Gaussian elimination can be used to compute the kernel. In each step, the kernel of similar matrices is required. There is an efficient method to construct the kernels with little effort [3]. Another important criterion is the length of the new cycle. In the following sections efficient approaches are presented to obtain the kernel of cycle-member incidence matrix and finding shortest admissible cycles.

The present method is efficient, and makes a fast and economical generation of suboptimal cycle basis feasible, and a complete automated analysis of a semi-rigid frame can easily be performed. The cycle basis selection algorithm leads to the formation of minimal cycle bases for graphs, and for practical models, this algorithm leads to the formation of a suboptimal cycle basis. The formation of self-equilibrating stress systems on the element of the selected cycle basis leads to the formation of a highly sparse matrix, making an efficient flexibility analysis of semi-rigid frame structures feasible.

1

Kaveh A. "Structural Mechanics: Graph and Matrix Methods", Research Studies Press, Exeter, U.K., 3rd edition, 2004.

2

Kaveh A. "Optimal Structural Analysis", Research Studies Press, Somerset, U.K., 1997.

3

Berger, F. Gritzmann P. and Sven de Vries, "Minimum cycle bases for network graphs", Algorithmica, No. 1, 2004;40:51-62. doi:10.1007/s00453-004-1098-x

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)