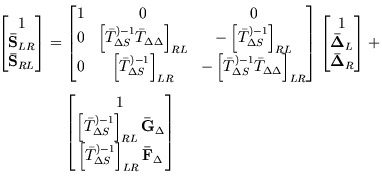engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
Transport Matrix Based Dynamic Stiffness Matrix of a Circular Helicoidal Bar
Department of Civil Engineering, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
With reference to a helicoidal bar [1] with helix angle
![]() and opening angle
and opening angle ![]() , the
position vector
, the
position vector
![]() in rectangular coordinates is used with Fernet's formulas [3] to
yield the following matrix relationship
in rectangular coordinates is used with Fernet's formulas [3] to
yield the following matrix relationship
| (7) |
in which a state sub-vector
The governing scaled differential matrix equation for a helicoid differential
segment of mass ![]() per unit length and mass moment of inetia
per unit length and mass moment of inetia ![]() , is written [4] as
, is written [4] as
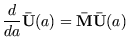 |
(8) |
and the Cayley-Hamilton Theorem [3,5] is used to write the solution of the equation in terms of powers of a (12x12) matrix
from which the (12x1) scaled transport load vector
The above condensed matrix form is identified as the stiffness matrix equation for a helicoid beam segment. The two sub-vectors of the column vector on the right hand-side of equation (10) represent stiffness load vectors
The computer code in its present form has been designed to construct and solve
the scaled matrix equations (10) for a stand-alone helicoidal beam instead of using
less specialized isoparametric finite elements [2]. It requires only few parameters to
define the geometry and material characteristics of the beam. The structural
geometry is defined by radius R, helix angle
![]() , and the cross section properties (i.e.:
A, Ix, Iy and Iz),
while the material properties are defined by material constants E
and
, and the cross section properties (i.e.:
A, Ix, Iy and Iz),
while the material properties are defined by material constants E
and ![]() . As such, the code is user-friendly and reduces the utilization-hardship that is
invariably present in almost all general purpose computer programs. More-over, and
due to the low number of design variables, the code will also make the search
process for optimal designs simpler and short. The code is, therefore, strongly
recommended for implementation within a general purpose finite element code to
solve space structural analysis and/or design problems that involve helicoidal beams.
. As such, the code is user-friendly and reduces the utilization-hardship that is
invariably present in almost all general purpose computer programs. More-over, and
due to the low number of design variables, the code will also make the search
process for optimal designs simpler and short. The code is, therefore, strongly
recommended for implementation within a general purpose finite element code to
solve space structural analysis and/or design problems that involve helicoidal beams.
- 1
- A. Abdul-Baki, D. Bartel, "Analysis of Helicoidal Girders", Eng. J., ASCE, 84-99, 1969.
- 2
- K.J. Bathe, Finite Element Procedures, New York, Prentice-Hall, 1996.
- 3
- F.B. Hildebrand, Methods of Applied Mathematics, 2nd edition, Englewood Cliffs, New Jersey: Prentice Hall, 259-279, 1965.
- 4
- S.A. Alghamdi, J.J. Tuma, "Static Analysis of Helicoidal Bars", Proceedings, Fourth International Conference on Civil & Structural Engineering Computing, College University, 247-258, London, 19-21 September, 1989.
- 5
- S.A. Alghamdi, B.O. Elbedoor, "Dynamic Stiffness Matrix of a Circular Helicoidal Bar", CE-Graduate Report (unpublished), Department of Civil Engineering, King Fahd University of Petroleum & Minerals, Dhahran, 1992.
- 6
- S.A. Alghamdi, A.A. Boumenir, "Numerical Solution for the Differential Equations Governing the Free Vibrations of Space Helicoidal Bars", The Arabian Journal for Science and Engineering, 23, 183-193, 1998.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)