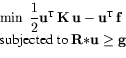Keywords: finite element method, saddle point problem, iterative methods, preconditioners, incomplete factorizations, contact problems.

The finite element method is an important tool used in the mechanical engineering design of contact problems. In this kind of problem the evolution of the stress distribution near the contact zone has to be obtained with high accuracy. Since the elastic bodies in contact can be under global sliding condition, in general, the meshes are non-conforming in the contact zone. Assuming elastic behavior of the solids in contact and small displacement hypothesis, the contact problem can be formulated as the minimization of a functional (total potential energy) under certain displacement constraints. A number of formulations have been developed to solve this problem using the finite element method [1]. In this paper the so called mortar method is used. The contact problem can be formulated as

where is the nodal displacement vector, is the stiffness matrix of the problem and is the equivalent nodal force corresponding to the external loads. The restriction equations due to contact of the bodies are imposed by means of matrix . Using the Lagrange multiplier method the following equations system is obtained

The coefficient matrix of this system is an indefinite matrix and so this is a saddle point problem. Moreover, this matrix typically is large and sparse and the system must be solved using iterative methods, usually Krylov algorithms. There is a wide bibliography related with the saddle point solvers [2].

Different preconditioned iterative methods to solve contact problems obtained from fretting-fatigue analysis have been compared in this work, including block diagonal preconditioners, indefinite preconditioners using the constraint equations and preconditioners based on Hermitian and skew-Hermitian parts of the matrix.

Firstly, a diagonal scaling and an augmented Lagrangian technique have been applied to the system (74) in order to obtain the following system

where , , and , with . is now a symmetric positive definite matrix.

We have considered different approximations of matrix , such as diag and incomplete Cholesky factorizations of with different threshold parameters , to construct block diagonal preconditioners. These preconditioners have been applied to the MINRES and SYMMLQ methods. The results obtained show that the block diagonal preconditioners using an incomplete Cholesky factorization of matrix with high threshold values (for example ) are recommended for the MINRES and SYMMLQ methods.

We have also considered the constraint preconditioner defined in [3,4], which allows for the utilization of the Conjugate Gradient method. The results thus obtained clearly improve those obtained without preconditioning even with a very basic preconditioner like CCG(I).

Finally, we have used the HSS preconditioner defined in [5] for different values of parameter . Low values of in the HSS preconditioner have shown to have an optimal performance.

In terms of accuracy, the CCG(I) method has shown to be most stable strategy.

1

P. Wriggers, Computational Contact Mechanics, John Wiley & Sons, Ltd., 2002.

2

M. Benzi, G.H. Golub, and J. Liesen, "Numerical Solution of Saddle Point Problems", Acta Numerica, 14, 1-137 (invited survey paper), 2005. doi:10.1017/S0962492904000212

3

C. Keller, N.I.M. Gould, and A.J. Wathen, "Constraint preconditioning for indefinite linear systems", SIAm J. Matrix Anal. Appl., 21, 1300-1317, 2000. doi:10.1137/S0895479899351805

4

N.I.M. Gould, M.E. Hribar, and J. Nocedal, "On the solution of equality constrained quadratic programming problems arising in optimization", SIAM J. Sci. Comput., 23, 1376-1395, 2001. doi:10.1137/S1064827598345667

5

M. Benzi, M.J. Gander, and G.H. Golub, "Optimization of the Hermitian and Skew-hermitian splitting iteration for saddle-point problems", BIT, 43, 881-900, 2003. doi:10.1023/B:BITN.0000014548.26616.65

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)