
engineering & technology publications
ISSN 1759-3158
COMPUTATIONAL STRUCTURES TECHNOLOGY
Research on Thin-Walled I-Beams Curved In-Plan
School of Civil and Environmental Engineering, The University of New South Wales, Sydney, Australia
Geometric nonlinearity arises because of the coupling of the primary actions and
deformations to produce second order effects. The primary actions (major axis bending
and torsion) cause primary and transverse deflections and primary twist deflections, as
well as secondary minor axis deformations, and when combined with the primary actions
these secondary deformations cause second order deflections. If ![]() and
and ![]() denote the
primary bending moment and torque respectively, then the coupling can be described
approximately by
denote the
primary bending moment and torque respectively, then the coupling can be described
approximately by
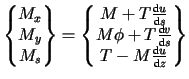 |
(1) |
where
Material nonlinearity arises owing to the yielding of the steel, to residual stresses induced during the manufacture of the member and to residual stresses that may be created during the curving process. The effects of the geometric nonlinearities can cause the deflections to grow rapidly, and when combined with the material nonlinearities they can cause early yielding of the member, particularly when the included angle within the curved beam is large.
In order to investigate the effects of these interactions, recourse needs to be made to a sophisticated numerical treatment that includes residual stresses and a nonlinear representation of the (small) strain (large) displacement relation [1]. Some numerical approaches are reviewed in the paper, as are some design procedures that have eventuated from these studies, and which are argued in the paper to be inaccurate. In the finite element procedure described by Pi et al. [1], it is shown that the sampling scheme used in other finite element packages leads to erroneous results as it does not correctly include the effects of the shear strains that develop due to torsion. The paper also compares the solutions of the numerical treatment with some recent experimental results, and the comparison is good.
A correct numerical analysis of I-beams curved in beam that accounts accurately for the material and geometric nonlinearities is still a research tool, and guidance need to be provided for structural designers. Because of this, the paper uses the finite element procedure [1] to conduct sufficient parameter studies to propose a design rule, and that which is chosen is consistent with the Australian steel structures standard [2], and which is also suitable for a number of other national design standards. A simple prescriptive equation for the strength interaction of primary bending and torsion actions is proposed, and which leads to the limiting case of lateral buckling of a straight beam when the included angle approaches zero and the torsion is eliminated. This limiting condition is not achieved by previous design suggestions.
- 1
- Y.-L. Pi, M.A. Bradford, N.S. Trahair, "Inelastic Analysis and Behavior of Steel I-Beams Curved In-Plan ", Journal of Structural Engineering, ASCE, 126(7), 772-779, 2000. doi:10.1061/(ASCE)0733-9445(2000)126:7(772)
- 2
- Standards Australia, "AS4100 Steel Structures ", S.A., Sydney, 1998.
purchase the full-text of this chapter (price £20)
go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £88 +P&P)