
engineering & technology publications
ISSN 1759-3158
INNOVATION IN COMPUTATIONAL STRUCTURES TECHNOLOGY
Non-Linear Vibration Modes of Plates and Shells
DEMEGI/IDMEC, Faculty of Engineering, University of Porto, Portugal
This lecture intends to provide a concise review on geometrically non-linear free
vibrations of plates and shells, and to present representative examples of non-linear
modes of vibration of these structures. To achieve the second aim, ![]() -version,
hierarchical finite elements for thin, isotropic, linear elastic, plates and shallow
shells are used. The plate element is similar to the one given in [2] and the shell
element essentially follows the lines of reference [3], but assuming thin shell theory.
Modal coordinates are employed in order to reduce the number of time domain
equations of motion. However, several modes are included, since severe reduction of
the number of coordinates would restrain the ability to describe the variation of the
mode shapes with the vibration amplitude.
-version,
hierarchical finite elements for thin, isotropic, linear elastic, plates and shallow
shells are used. The plate element is similar to the one given in [2] and the shell
element essentially follows the lines of reference [3], but assuming thin shell theory.
Modal coordinates are employed in order to reduce the number of time domain
equations of motion. However, several modes are included, since severe reduction of
the number of coordinates would restrain the ability to describe the variation of the
mode shapes with the vibration amplitude.
The equations of motion obtained can be written in a simplified way as follows
| (3) |
where
The harmonic balance method is applied, writing the modal coordinates as:
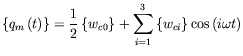 |
(4) |
and the resulting frequency domain equations are solved by a continuation method [4].
Non-linear modes of plates and shells are computed. Generally, the non-linear natural frequency of vibration is the frequency of the fundamental harmonic and is amplitude dependent. In shells, the non-linear natural frequency may increase or decrease with the vibration amplitude. On the other hand, numerical tests indicate that in perfect plates with fixed boundaries, the non-linear natural frequency increases with the vibration amplitude. However, other non-linear natural frequencies can be connected with non-fundamental harmonics, as occurs in the case of internal resonances. Internal resonances, that is, modal coupling between modes with resonance frequencies related by a rational number, are possible in plates and shells. They result in bifurcation points and in associated secondary branches, or in complex curvatures of the curves which relate the amplitude with the non-linear frequency of vibration.
Each harmonic of the periodic, free oscillations is connected with a non-linear mode shape that changes with the vibration amplitude, due to the variation of the stiffness and that tends towards a linear mode shape as the maximum amplitude displacement tends towards zero. For each harmonic, all points achieve the maximum displacement and the equilibrium position simultaneously. Internal resonances cause a strong variation of the shapes assumed by the panels during a period of vibration.
- 1
- R.M. Rosenberg, "On non-linear vibrations of systems with many degrees of freedom", Advances Applied Mechanics, 9, 155-242, 1966. doi:10.1016/S0065-2156(08)70008-5
- 2
- W. Han and M. Petyt, "Geometrically nonlinear vibration analysis of thin, rectangular plates using the hierarchical finite element method - I: The fundamental mode of isotropic plates", Computers and Structures, 63, 295-308, 1997. doi:10.1016/S0045-7949(96)00345-8
- 3
- P. Ribeiro, "A hierarchical finite element for geometrically non-linear vibration of doubly curved, moderately thick isotropic shallow shells", International Journal for Numerical Methods in Engineering, 56, 715-738, 2003. doi:10.1002/nme.585
- 4
- R. Lewandowski, "Computational formulation for periodic vibration of geometrically nonlinear structures - Part 2: Numerical strategy and examples", International Journal of Solids and Structures, 34, 1949-1964, 1997. doi:10.1016/S0020-7683(96)00126-6
purchase the full-text of this chapter (price £20)
go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £95 +P&P)