Keywords: finite elements, B-splines, NURBS, structural vibrations.

In anticipation of the future in which Computational Geometry will play a more prominent role in Computational Structures Technology, we present an introduction to basic concepts of Isogeometric Analysis. NURBS (non-uniform rational B-splines) are employed to instantiate the Isogeometric Analysis concept. These enable high-precision geometry modeling and vastly simplify refinement strategies. NURBS are a standard CAD technology and have the potential for better integrating analysis with geometry. Applications to structural vibration problems indicate NURBS are much better behaved than standard finite elements.

The concept of Isogeometric Analysis introduced by Hughes, Cottrell and Bazilevs [3] and expanded by Cottrell et al. [2] and Bazilevs et al. [1] is a new method for the analysis of problems governed by partial differential equations such as, for example, solids, structures and fluids. Logically, it is a generalization of finite element analysis, containing it as a special case. Isogeometric Analysis has many features in common with the finite element method and some features in common with meshless methods. However, it is more geometrically based and takes inspiration from Computer Aided Design (CAD). A primary goal is to be geometrically precise no matter how coarse the discretization. Another goal is to simplify mesh refinement by eliminating the need for communication with the CAD geometry once the initial mesh is constructed. Yet another goal is to better integrate the mesh generation process with CAD. In this work we introduce ideas in pursuit of these goals.

The body of this paper begins with a tutorial on B-splines, followed by one on NURBS (non-uniform rational B-splines). We then describe an analysis framework based on NURBS. This is followed by some sample one-dimensional problems of structural vibrations. Elementary model problems for a rod and thin beam are solved numerically. The new k-method is shown to provide more robust and accurate frequency spectra than typical higher-order finite elements (i.e., the p-method). Particularly intriguing is the possibility of eliminating "optical" branches of frequency spectra through the use of nonlinear parameterizations of the geometrical mapping [2]. Optical branches have been identified as causes of severe accuracy degradation in higher modes and Gibbs phenomena in wave propagation. We conclude with a discussion the NASA Aluminum Testbed Cylinder (ATC). An exact geometrical model of the ATC is created and analysis is performed. Comparison is made with experimental results and good agreement is attained.

The analytical and geometrical precision of Isogeometric Analysis demonstrates the power and future potential of Computational Geometry in Computational Structures Technology.

1

Y. Bazilevs, L. Beirao de Veiga, J.A. Cottrell, T.J.R. Hughes, and G. Sangalli. Isogeometric analysis: approximation, stability and error estimates for 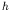-refined meshes. To appear in Mathematical Models and Methods in Applied Sciences. ICES Report 06-04, University of Texas, Austin: URL

2

J.A. Cottrell, A. Reali, Y. Bazilevs, and T.J.R. Hughes. Isogeometric analysis of structural vibration. To appear in Computer Methods in Applied Mechanics and Engineering. ICES Report 05-27, University of Texas, Austin: URL

3

T.J.R. Hughes, J.A. Cottrell, and Y. Bazilevs. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194:4135-4195, 2005. doi:10.1016/j.cma.2004.10.008

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £95 +P&P)