Keywords: simulation of lateral deflection, single vertical pile, polynomial, lateral load, least squares adjustment method.

This paper presents a scheme for simulation of lateral deflection for a single vertical pile subjected to lateral load by means of polynomial. At selected locations along the pile shaft, lateral deflection at each location is represented by a polynomial with degree of . The simulation needs two measured values. One is the distance between the selected location and the pile head, and another is its corresponding magnitude of lateral deflection. Use of polynomial as an interpolation tool to simulate the lateral deflection measured from field load test has two main practical tasks [1], they are (1) given some function and an interval, find a program that gives an adequate approximation to the function for any value in interval; and (2) given a collection of data points, estimate the value of function at some domain point not among the collected data points. When redundant data exist, an adjustment is necessary so as to get a unique solution to the problem at hand. The least squares adjustment method assuming that all observations are uncorrelated and of unequal precision [2] is adopted in this analysis.

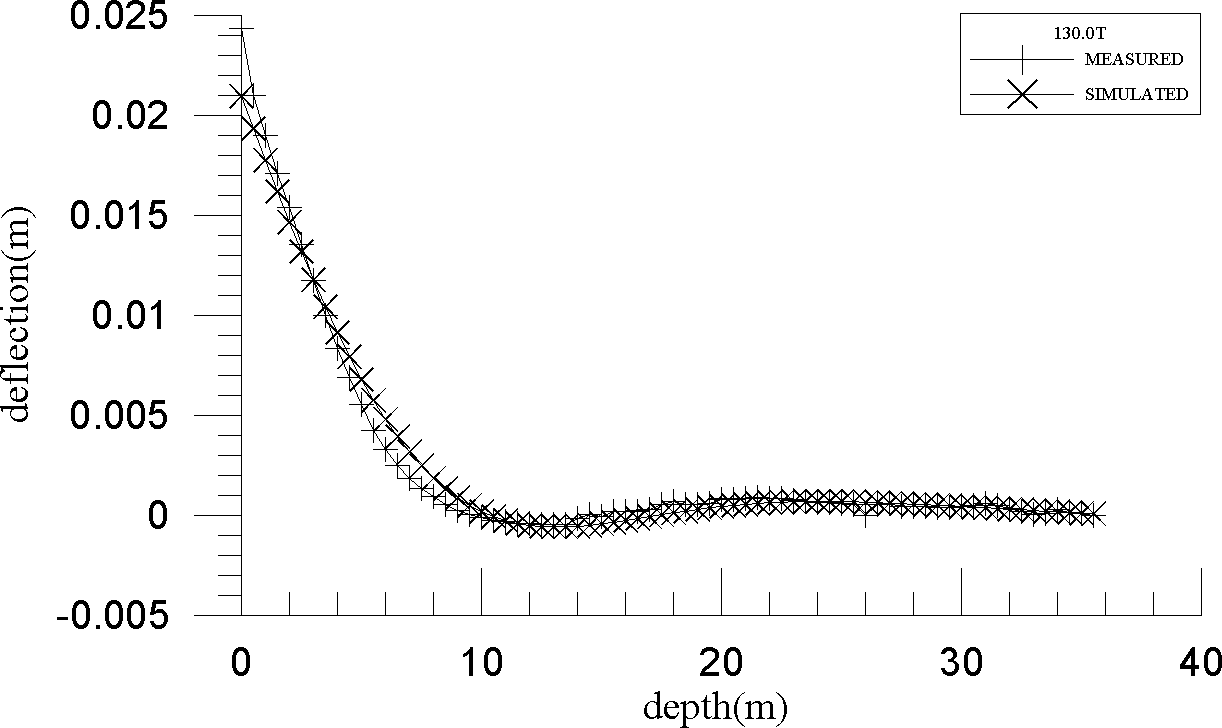
Schemes have been proposed for single vertical pile with free-head and fixed head conditions. In this analysis, the distribution of lateral deflection for a single pile subjected to lateral load is given by a polynomial. Practitioners found that when the degree of the approximating polynomial is moderate (say 8) to large, solution of the normal equation for the polynomial coefficients often leads to seriously erroneous answers [1]. As a consequence, the computed vector of unknown coefficients tends to differ substantially from its exact solution. Should a vector of unknown coefficients can be determined, residual exists for any approximation. In the method of least squares, the discrepancy of the data points and approximating polynomial is measured by the sum of the squared residuals. For the uncorrelated observations of unequal precision, the criterion calls for minimization of the weighted function. A weighted matrix is introduced to bring the reliability of every equation into account. If the exact unknown coefficients vector can be obtained, the approximate lateral deflection can be uniquely predicted by the polynomial. The distribution of slope variation, moment, shear force, and soil reaction along the depth of pile can be subsequently determined by differentiating of polynomial of lateral deflection. In Figure 55.1 a comparison of measured and simulated lateral deflection for pile head load 130.0T is shown. The results of analysis indicate the suitability of this proposed scheme.

1

Yakowitz, S. and Szidarovszky, F., "An Introduction to Numerical Computations", Macmillan Publishing Company, Chapter 3 to 6, 113-358, 1989.

2

Mikhail, E.M., and Gracie, G., "Analysis and Adjustment of Survey Measurements", Van Nostrand Reinhold, Chapter 3 to 4, 31-105, 1981.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £85 +P&P)