
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE THIRD INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Modelling of High Pressure Die Casting using the CSPH Method
Institute of Numerical Methods, University of Wales, Swansea, United Kingdom
Validating the numerical simulations with experimental data is very difficult because of the speeds, pressures, temperatures, thinness of the die cavity and the bulk of the die. Clearly, numerical modelling offers a better and inexpensive way to analyse these complex metal flows and to optimise the gating system and the geometry of the die. Eulerian based techniques such as the finite element and finite volume methods have been used to model low pressure die casing processes [9,10]. However, for high pressure, high velocity, die casting these methods are unable to accurate simulate the complex free surface behaviour.
The Lagrangian based Corrected Smooth Particle Hydrodynamics (CSPH) [11,12] method is
used to model the numerical simulation of the high pressure die casting process. CSPH does
not use a grid to compute partial derivatives. The variables determining the flow, such as
pressure and velocity, are localised on a set of particles which move with the flow. This
property enables the technique to simulate complex free surfaces including fragmentation and
droplet formation. The CSPH method is based around the reproducing kernel function in
which for any given function ![]() can be approximated by the following integral as,
can be approximated by the following integral as,
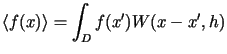 d d |
(39.1) |
where
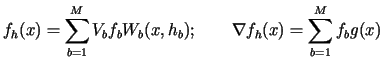 |
(39.2) |
where
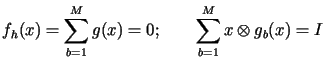 |
(39.3) |
A number of authors have described various methodologies that can be adopted to fulfil the above conditions [8,11,12] . This paper focuses on the application of the CSPH method to simulate the high pressure die casting process. A detailed description of the formulation of the governing equations is presented with several numerical simulations to demonstrate the performance of the proposed computational model.
- 1
- L.B. Lucy, "A numerical approach to the testing of the fission hypothesis", Astro. J., 82 1013, (1977). doi:10.1086/112164
- 2
- R.A. Gingold and J.J. Monaghan, "Smooth Particle Hydrodynamics: Theory and Application to Non- Spherical Stars", Mon. Not. R. Astron. Soc., 181, 375, (1977).
- 3
- J.J. Monaghan, "An introduction to SPH", Comput. Phys. Comm., 48, 89-96, (1988). doi:10.1016/0010-4655(88)90026-4
- 4
- J.J. Monaghan, "Smooth Particle Hydrodynamics", Annu. Rev. Astron. Astrophys., 30, 543, (1992). doi:10.1146/annurev.aa.30.090192.002551
- 5
- J.J. Monaghan, "Simulating Free Surface Flows with SPH", J. Comput. Phys., 110, 399, (1994). doi:10.1006/jcph.1994.1034
- 6
- L.D. Libersky, A.G. Petschek, T.C. Carney, J.R. Hipp, F.A. Allahadi, "High Strain Lagrangian Hydrodynamics", J. Comput. Phys., 109, 67, (1993). doi:10.1006/jcph.1993.1199
- 7
- W.K. Liu, S. Jun, Y.F. Zhang, "Reproducing Kernel Particle Methods", Int. J. Num. Meth. Engrg., bf 20 (1995). doi:10.1002/nme.1620381005
- 8
- R.W. Randles, L.D. Libersky, "Smooth Particle Hydrodynamics: Some Recent Improvements and Applications", Comput. Methds Appl. Mech. Engrg., 139, 376, (1996). doi:10.1016/S0045-7825(96)01090-0
- 9
- R.W. Lewis, K. Ravendran, "Finite element simulation of metal casting", Int. J. Num. Meth. Engrg, 47, 29- 59 (2000). doi:10.1002/(SICI)1097-0207(20000110/30)47:1/3<29::AID-NME760>3.0.CO;2-X
- 10
- W-S. Hwang, R.A. Stoehr, "Modelling fluid flow", Metals handbook Casting ASM International, 15, 867- 876, (1988)
- 11
- J. Bonet, T.S.L. Lok, "Variational and Momentum Aspects of Smooth Particle Hydrodynamics Formulations", Comput. Methds Appl. Mech. Engrg., 180, 97-115, (1999). doi:10.1016/S0045-7825(99)00051-1
- 12
- J. Bonet, S. Kulasegarm, "Correction and Stabilization of Smooth Particle Hydrodynamics Method with Applications in Metal Forming Simulations", Int. J. Num. Meth. Engng., 47, 1189-1214, (2000). doi:10.1002/(SICI)1097-0207(20000228)47:6<1189::AID-NME830>3.0.CO;2-I
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £85 +P&P)