
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE SIXTH INTERNATIONAL CONFERENCE ON THE APPLICATION OF ARTIFICIAL INTELLIGENCE TO CIVIL AND STRUCTURAL ENGINEERING
Genetic Algorithm Trained Counter-Propagation Neural Net in Structural Optimization
Department of Civil Engineering, Shahid Bahonar University of Kerman, Iran
Counter-Propagation neural network is a combination of two well-known
algorithms: the self-organizing map of Kohonen and the Grossberg outstars. In the
process of training, the weight matrices are computed internally. To define criteria
for proximity of weight matrices in the Kohonen layer and input vector, parameter
![]() is defined as below [1,2]:
is defined as below [1,2]:
| (36.1) |
For the learning coefficient, Hecht-Neilsen suggests a number in the range
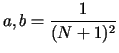 |
(36.2) |
parameters
| (36.3) |
a,b : Learning coefficients; N: Number of iterations
Genetic Algorithms are computationally simple, but powerful in their search for improvement, and they are not limited by restrictive assumptions about the search space, such as continuity or existence of derivatives. Genetic Algorithms are search procedures based on the mechanics of natural genetic and natural selection. They combine the concept of the artificial of the artificial survival of the fittest with genetic operators abstracted from nature to form a powerful search mechanism[4,5]. The main objective is error reduction of the Counter-Propagation Neural net (CPN) response by application of the Genetic Algorithms. Genetic operators are applied so that the net is improved and error on the output units is reduced. By error minimizing of the net response and generating proper genetic training pairs, the overall performance of the net as compared with random training pairs is improved. The optimim design of a three spans girder with uniform load a cocentrated load at each mid span was considered. The results show that modifying parametes a and b, the learing coefficients of the Kohonen and the Grossberg layers will improve the net efficiency. To investigate the effects of other alternatives on the CPN neural net response, GAs are used in the training process. Based on the minimization of the error function and application of the genetic operators, Reproduction, Crossover, and Mutation proper net response is achieved. Stress analysis of plane and space trusses is considered, the overall performance of the net has been improved.
- 1
- L. Szewczyk and P. Hajela, "Neural Network Approximations in a Simulated Annealing Based Optima Structural Design", Structural Optimization, 4:90-98, 1992. doi:10.1007/BF01759922
- 2
- A. Iranmanesh, and A. Kaveh, "Structural Optimization by Gradient-Based Neural Networks", Int. J. Numer. Meth. Engng. 46, 297-311, 1999. doi:10.1002/(SICI)1097-0207(19990920)46:2<297::AID-NME679>3.3.CO;2-3
- 3
- H. Adeli and H. S. Park, "Counterpropagation Neural Networks in Structural Engineering", Journal of Structural Engineering, 121: 1205-1211, 1995. doi:10.1061/(ASCE)0733-9445(1995)121:8(1205)
- 4
- S. J. Wu and P. T. Chow, "Integrated Discrete and Configuration Optimization of Trusses Using Genetic Algorithms", Computers & Structures, Vol. 55, No.4, 695-702, 1995. doi:10.1016/0045-7949(94)00426-4
- 5
- H. Adeli, N.T. Cheng, "Integrated Genetic Algorithm for Optimization of Space Structures", J. Aerosp. Engrg., ASCE, Vol. 6, No. 4, 315-329, 1993. doi:10.1061/(ASCE)0893-1321(1993)6:4(315)
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £78 +P&P)